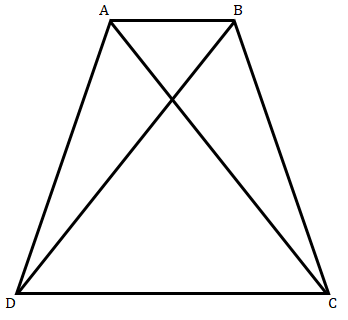
梯形 ABCD 的对角线 AC 和 BD 相交于点 O，其中 AB ∥ DC。利用两个三角形的相似性判别法，证明 OA/OC = OB/OD。
"\n

已知

梯形 ABCD 的对角线 AC 和 BD 相交于点 O，其中 AB ∥ DC。

要求

我们需要证明 OA/OC = OB/OD。

解答

在△AOB 和△COD 中，

∠AOB = ∠COD（对顶角相等）

∠OAB = ∠OCD （AB ∥ DC，内错角相等）

因此，

△AOB ∽ △COD

这意味着，

OA/OC = OB/OD （对应边成比例）

证毕。

教程点

更新于： 2022年10月10日

57 次浏览

开启你的职业生涯

通过完成课程获得认证

开始学习