将一条长度为14厘米的线段按2:5的比例进行内分。并说明你的作图理由。

已知

一条长度为14厘米的线段。

 需要做的

我们需要将一条长度为14厘米的线段按2:5的比例进行内分。

解：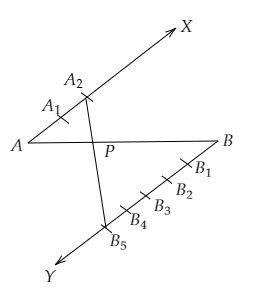

作图步骤

(i) 画一条线段$AB = 14\ cm$。

(ii) 画一条射线$AX$，与$AB$成锐角。

(iii) 从$B$点画另一条射线$BY$，与$AX$平行。

(iv) 在$AX$上截取两等份，在$BY$上截取五等份。

(v) 连接$A_2$和$B_5$，交$AB$于点$P$。

$P$点即为将$AB$线段按2:5的比例进行内分所得的点。 

证明：在$\triangle AA_2P$和$\triangle BB_5P$中，

$\angle A_2AP = \angle PBB_5$              ($\angle ABY = \angle BAX$)

$\angle APA_2 = \angle BPB_5$      (对顶角)

因此，根据AA相似性定理，

$\triangle AA_2P \sim \triangle BB_5P$

这意味着：

$\frac{AA_2}{BB_5} = \frac{AP}{BP}$

$\frac{AP}{BP} = \frac{2}{5}$ 

更新于：2022年10月10日

70 次浏览

开启你的职业生涯

完成课程获得认证

开始学习
广告