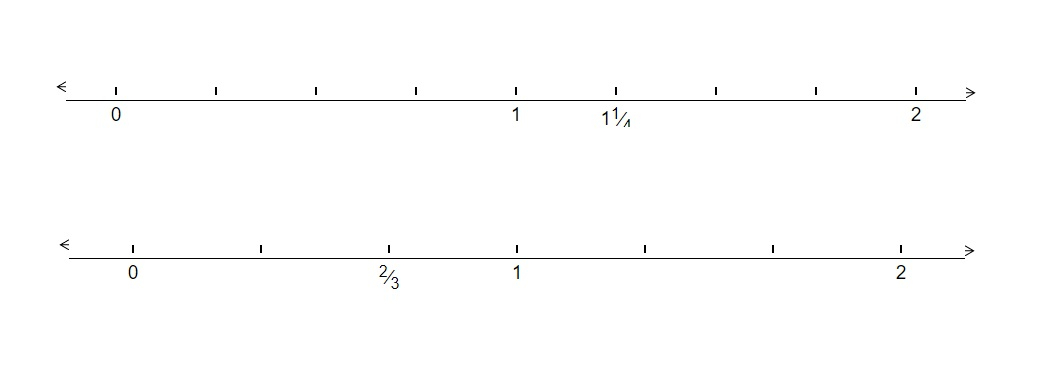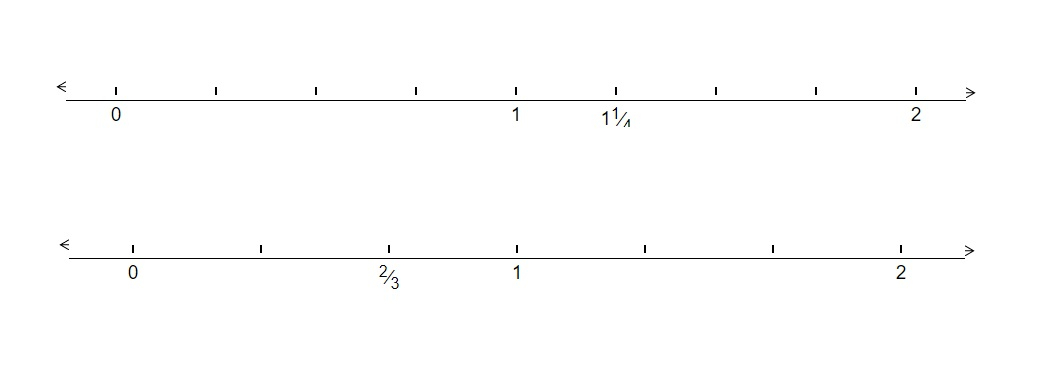如何在数轴上比较$\frac{5}{4}$和$\frac{2}{3}$？
已知
给定的数字是$\frac{5}{4}$和$\frac{2}{3}$。
要求
我们必须在数轴上比较给定的数字。
解答
为了在数轴上比较$\frac{5}{4}$和$\frac{2}{3}$，需要将它们表示在数轴上。
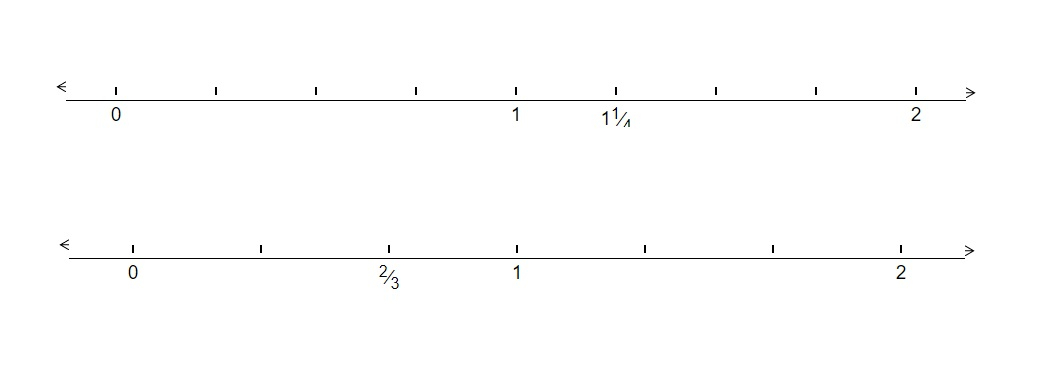
从图中可以看出，$\frac{2}{3}$位于0和1之间。
从图中可以看出，$\frac{5}{4}$位于1和2之间。
因此，
$\frac{5}{4}$大于$\frac{2}{3}$。
- 相关文章
- 在数轴上表示$\frac{4}{3}$和$\frac{-2}{9}$。
- 在数轴上显示以下数字。每个例子都画一条单独的数轴。(1) $\frac{3}{2}, \frac{5}{2},-\frac{3}{2}$。(2) $\frac{7}{5}, \frac{-2}{5}, \frac{-4}{5}$。(3) $\frac{-5}{8}, \frac{11}{8}$。(4) $\frac{13}{10}, \frac{-17}{10}$。
- 画出数轴并在其上定位点：(a) \( \frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{4}{4} \)(b) \( \frac{1}{8}, \frac{2}{8}, \frac{3}{8}, \frac{7}{8} \)(c) \( \frac{2}{5}, \frac{3}{5}, \frac{8}{5}, \frac{4}{5} \)
- 在数轴上表示$\frac{-5}{4}$。
- 解表达式:$\frac{5}{3}+\frac{4}{3}-\frac{4}{2}+\frac{4}{2} $
- 在数轴上表示以下数字：(i) $\frac{-4}{7}$(ii) $\frac{-2}{5}$
- 化简：(i) \( \frac{-3}{2}+\frac{5}{4}-\frac{7}{4} \)(ii) \( \frac{5}{3}-\frac{7}{6}+\frac{-2}{3} \)(iii) \( \frac{5}{4}-\frac{7}{6}-\frac{-2}{3} \)(iv) \( \frac{-2}{5}-\frac{-3}{10}-\frac{-4}{7} \)(v) \( \frac{5}{6}+\frac{-2}{5}-\frac{-2}{15} \)(vi) \( \frac{3}{8}-\frac{-2}{9}+\frac{-5}{36} \)
- 画一条数轴，并在其上定位以下点：$\frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{4}{4}$
- 在数轴上表示数字$\frac{2}{4}$。
- 在下列各项中，哪个更大：(i) $\frac{2}{3},\ \frac{5}{2}$(ii) $-\frac{5}{6},\ -\frac{4}{3}$(iii) $-\frac{3}{4},\ \frac{2}{-3}$(iv) $-\frac{1}{4},\ \frac{1}{4}$(v) $-3\frac{2}{7\ },\ -3\frac{4}{5}$
- 在数轴上显示$\frac{3}{5}$。
- 化简下列式子：$-\frac{2}{3}+(\frac{2}{3}+\frac{4}{5})$
- 解下列式子：$(\frac{5}{3})^4 \times (\frac{5}{3})^4 \div (\frac{5}{3})^2$。
- 解(a) \( \frac{2}{3}+\frac{1}{7} \)(b) \( \frac{3}{10}+\frac{7}{15} \)(c) \( \frac{4}{9}+\frac{2}{7} \)(d) \( \frac{5}{7}+\frac{1}{3} \)(e) \( \frac{2}{5}+\frac{1}{6} \)(f) \( \frac{4}{5}+\frac{2}{3} \)(g) \( \frac{3}{4}-\frac{1}{3} \)(h) \( \frac{5}{6}-\frac{1}{3} \)(i) \( \frac{2}{3}+\frac{3}{4}+\frac{1}{2} \)(j) \( \frac{1}{2}+\frac{1}{3}+\frac{1}{6} \)(k) \( 1 \frac{1}{3}+3 \frac{2}{3} \)(l) \( 4 \frac{2}{3}+3 \frac{1}{4} \)(m) \( \frac{16}{5}-\frac{7}{5} \)(n) \( \frac{4}{3}-\frac{1}{2} \)
- 在数轴上，下列分数中哪个更接近零？$\frac{3}{4}$或$\frac{3}{5}$
数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学