化简并验证当 $p=1$ 时的结果。$4 p^{3} \times 3 p^{4} \times( -p^{5})$
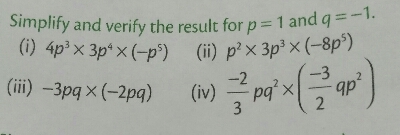"\n

已知：$4p^{3}\times 3p^{4}\times( -p^{5})$

要求：化简并验证当 $p=1$ 时的结果。

解答

$4p^{3}\times 3p^{4}\times( -p^{5})$

$\Rightarrow 4p^{3}\times 3p^{4}\times( -p^{5})=4\times3\times p^{3}\times p^{4}\times p^{5}$

$\Rightarrow 4p^{3}\times 3p^{4}\times( -p^{5})=-12p^{3+4+5}$                               [$\because a^m\times a^n=a^{m+n}$]

$\Rightarrow 4p^{3}\times 3p^{4}\times( -p^{5})=-12p^{12}$

验证

$L.H.S.=4p^{3}\times 3p^{4}\times( -p^{5})$

$=4\times 1^3\times 3\times1^4\times ( -1^5)$

$=-12$

$R.H.S.=-12p^{12}$

$=-12\times 1^{12}$

$=-12$

因此，$L.H.S.=R.H.S.$，验证正确。

Tutorialspoint

更新于： 2022年10月10日

浏览量：111

开启你的 职业生涯

通过完成课程获得认证

开始学习