数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究使用连续放大在数轴上想象 \( 3.765 \)。
已知
已知数字为 $3.765$。
待做
我们必须使用连续放大在数轴上想象 $3.765$ 的表示。
求解
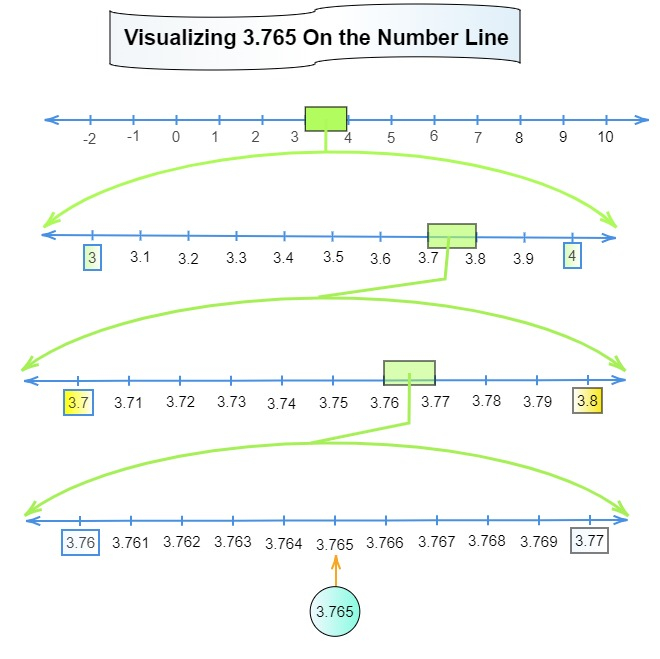
$3.765$ 介于 3 和 4 之间。
所以，我们将数轴分成 10 等份，并标记每个刻度点。3 右侧的第一个标记将是 $3.1$，后面是 $3.2$，以此类推。
4 左侧的点将是 $3.9$。
以上内容的放大视图表明 $3.765$ 介于 3.7 和 3.8 之间。
将 3.7 和 3.8 之间的线段分成 10 等份。
第一部分将是 3.71，后面是 3.72，以此类推。
以上内容的放大视图表明 $3.765$ 介于 3.76 和 3.77 之间。
将 3.76 和 3.77 之间的线段分成 10 等份。
第一部分将是 3.761，后面是 3.762，以此类推。
上述内容的放大视图将显示 $3.765$ 位于 3.76 和 3.77 之间，如下图所示。
更新于： 2022 年 10 月 10 日
106 次浏览
广告