平行线及其角的关系

---

引言

平行线是指在任何点都不会相交的线，两条线之间的距离相同。在几何学中，直线可以是相交线或不相交线。相交线彼此形成一个角，而不相交线彼此不形成任何角。平行线是不相交的线。平行线上的每个点与其在另一条线上对应的点等距。相交线在彼此之间形成 0 度到 360 度的角。在二维平面上，两条或多条线在几何学中可以相交、平行和垂直。线可以定义为垂直、平行、横截等。在本教程中，我们将了解平行线、横截线、平行线和横截线形成的角、同位角、内错角和外错角。我们还将学习关于横截线同侧的角以及一些关于这些主题的解题示例。

平行线

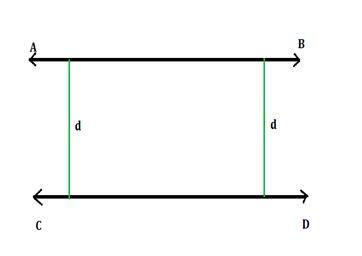
如果二维平面上的两条线即使延伸到无限远也不会相交，则这些线称为共面线或平行线。换句话说，如果这些线上的每个点与其在该平面上对应的点等距，则称这些线为平行线。

横截线

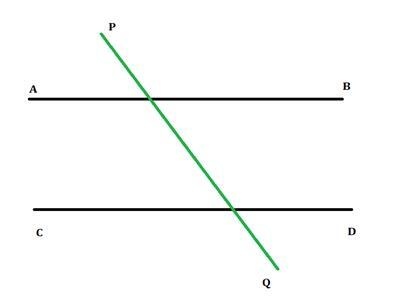
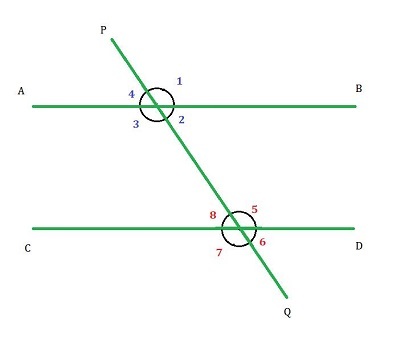
如果二维平面上的两条平行线被第三条线在两个不同的点处相交，则第三条线称为横截线。如图所示，横截线 PQ 在两个点处与线 AB 和 CD 相交。横截线与每条线形成八个不同的角，我们将在后面进一步讨论。

平行线和横截线形成的角

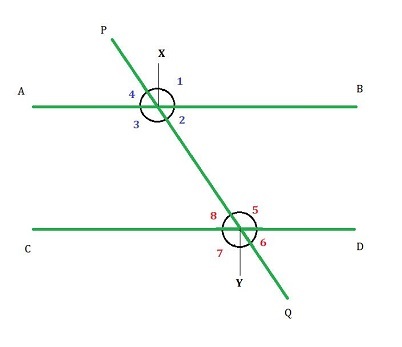
考虑下图。在图中，线 AB 平行于线 CD，横截线 PQ 穿过平行线。横截线在 X 点与线 AB 相交，在 Y 点与线 CD 相交。如图所示，横截线与线 AB 和 CD 形成八个角。这些角彼此之间存在一些关系，这有助于我们确定线之间的角。

横截线形成的不同类型的角将在后面讨论。

同位角

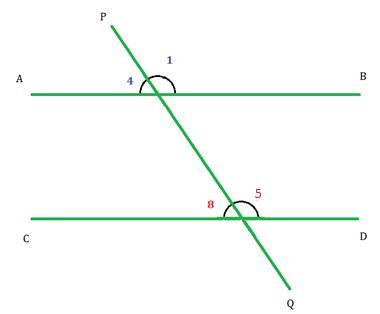
横截线在第一条线上形成的外角和横截线在第二条线上形成的内角在横截线的同一侧被称为同位角。在下图中，$\mathrm{\angle1}$ 是 $\mathrm{\angle5}$ 的同位角，$\mathrm{\angle4}$ 是 $\mathrm{\angle8}$ 的同位角。并且平行线形成的同位角彼此相等；因此，

$$\mathrm{\angle1\:=\:\angle5}$$

$$\mathrm{\angle4\:=\:\angle8}$$

类似地，横截线在第一条线上形成的内角和横截线在第二条线上形成的外角在横截线的同一侧被称为同位角。

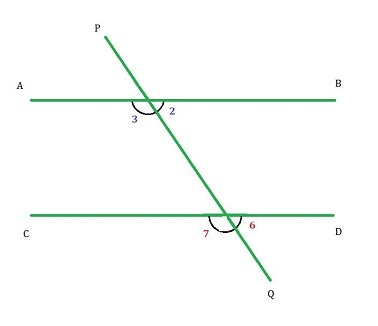
因此，$\mathrm{\angle2\:=\:\angle6}$

$\mathrm{\angle3\:=\:\angle7}$

内错角和外错角

与同位角相反，内错角和外错角包括横截线两侧的内角和外角。

内错角

横截线在两条平行线上形成的位于横截线异侧的内角称为内错角。如图所示，$\mathrm{\angle2}$ 是 $\mathrm{\angle8}$ 的内错角，$\mathrm{\angle3}$ 是 $\mathrm{\angle5}$ 的内错角。

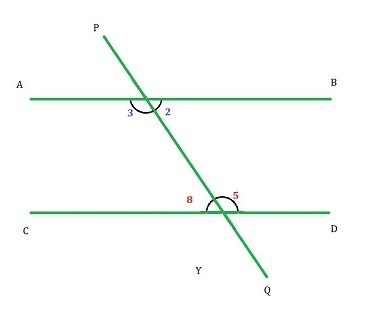
平行线形成的内错角相等。

因此，$\mathrm{\angle2\:=\:\angle8}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\angle3\:=\:\angle5}$

外错角

横截线在其任一侧形成的外角称为外错角。如图所示，$\mathrm{\angle1}$ 是 $\mathrm{\angle7}$ 的外错角，$\mathrm{\angle4}$ 是 $\mathrm{\angle6}$ 的外错角。

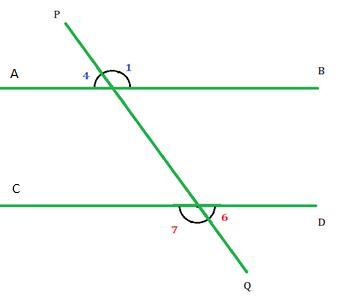
平行线形成的外错角相等。

因此， $\mathrm{\angle1\:=\:\angle7}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\angle4\:=\:\angle6}$

横截线同侧的角

横截线在两条平行线上形成的位于横截线同侧的内角称为同旁内角。如图所示，$\mathrm{\angle2}$ 是 $\mathrm{\angle5}$ 的同旁内角，$\mathrm{\angle3}$ 是 $\mathrm{\angle8}$ 的同旁内角。

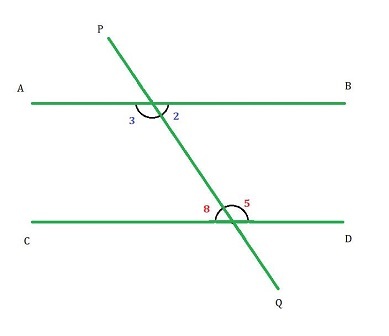
如果一条横截线与两条平行线相交，则每对同旁内角互补。

因此， $\mathrm{\angle2\:+\:\angle5\:=\:180°\:\:\:\:\angle3\:+\:\angle8\:=\:180°}$

对顶角

横截线与两条平行线在两个不同点相交形成的每个角与其在同一条线上异侧的对角互为对顶角。如图所示，$\mathrm{\angle1}$ 与同一条线上的 $\mathrm{\angle3}$ 互为对顶角，同样，$\mathrm{\angle2}$ 和 $\mathrm{\angle4}$，$\mathrm{\angle5}$ 和 $\mathrm{\angle7}$，以及 $\mathrm{\angle6}$ 和 $\mathrm{\angle8}$ 互为对顶角。

对顶角彼此相等。

因此， $\mathrm{\angle1\:=\:\angle3\:,\:\angle2\:=\:\angle4\:,\:\angle5\:=\:\angle7\:,\:\angle6\:=\:\angle8}$

解题示例

1) 在下图中，线 AB 平行于线 CD。横截线 PQ 在 X 和 Y 点与线相交。如果 $\mathrm{\angle\:AXP\:=\:60°}$，则求角 $\mathrm{\angle\:PYD}$。

答 - 已知，$\mathrm{\angle\:AXP\:=\:60°\:,\:AB\:\:\:\rVert\:\:CD}$

根据横截线的性质，对顶角彼此相等。因此，

$$\mathrm{\angle\:AXP\:=\:\angle\:QXB}$$

$$\mathrm{\angle\:QXB\:=\:60°}$$

根据横截线同侧角的性质，

$$\mathrm{\angle\:QXB\:+\:\angle\:PYD\:=\:180°}$$

$$\mathrm{60°\:+\:\angle\:=\:180°}$$

$$\mathrm{\angle\:PYD\:=\:120°}$$

2) 在给定图中求 x，其中线 AB 和 CD 是平行线，PQ 是穿过它们的横截线。已知，$\mathrm{\angle\:QXB\:=\:72°}$

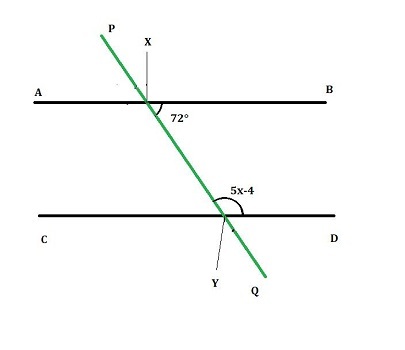
答 - 已知 $\mathrm{\angle\:QXB\:=\:72°\:,\:AB\:\:\:\rvert\:\:\:CD\:,\:\angle\:PYD\:=\:5x\:-\:4}$

根据横截线同侧内角的性质，

$$\mathrm{\angle\:QXB\:+\:\angle\:PYD\:=\:180°}$$

$$\mathrm{72°\:+\:5x\:-\:4\:=\:180°}$$

$$\mathrm{5x\:-\:4\:=\:108°}$$

$$\mathrm{5x\:=\:112°}$$

$$\mathrm{x\:=\:224°}$$

结论

线可以定义为垂直、平行、横截等。平行线是不相交的线。平行线上的每个点与其在另一条线上对应的点等距。如果二维平面上的两条平行线被第三条线在两个不同的点处相交，则第三条线称为横截线。横截线在第一条线上形成的外/内角和横截线在第二条线上形成的内/外角在横截线的同一侧被称为同位角。横截线在两条平行线上形成的位于横截线异侧的内/外角称为内错角/外错角。当横截线与其中一条平行线相交时，彼此相对的角称为对顶角。

常见问题

1. 横截线穿过两条平行线时会形成多少个角？

横截线穿过两条平行线时会形成八个角。

2. 什么是同位角？

横截线在第一条线上形成的外/内角和横截线在第二条线上形成的内/外角在横截线的同一侧被称为同位角。

3. 内角之间是什么关系？

横截线同侧的内角互补，即它们的和等于 180°。横截线异侧的内角相等。

4. 什么是对顶角？

当横截线与其中一条平行线相交时，彼此相对的角称为对顶角。

5. 什么是内错角和外错角？

横截线在两条平行线上形成的位于横截线异侧的内角称为内错角。