回转半径

---

简介

物体的回转半径通常定义为围绕其旋转轴的径向距离。这个距离与一个点的转动惯量相关联。如果将物体的总质量集中在该点，则该转动惯量将等于该特定物体的实际质量分布。

回转半径在日常生活中各个学科中都很有用，尤其是在工程领域。在现实生活中，它用于研究柱的刚度。回转半径也称为回旋半径。

回转半径是什么意思？

物体的回转半径通常表示特定物体绕其特定轴的转动惯量。但是，它可以被定义为不同的概念，因此需要注意的是，回转半径可以被认为是物体形心（Shaheen 等人，2018）的一个假设距离。

这个形心与横截面积相关联，该面积被认为集中在一个特定点，以获得相同的转动惯量。回转半径通常用 k 表示。

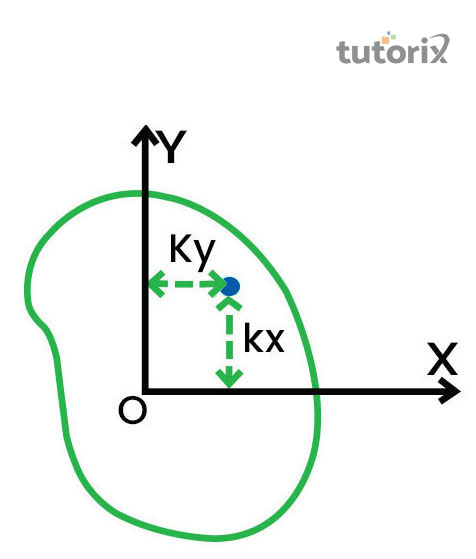
图 1：回转半径

回转半径的数学描述是什么？

在数学上，可以注意到回转半径与特定物体各部分的均方根距离相关联。它可以是从特定轴的质心，取决于数学应用的相关性（Khatiwada，2020）。需要注意的是，它是质量点到旋转轴的垂直距离（Haydukivska 等人，2020）。

个人可以将运动点的轨迹表示为一个物体。在这种情况下，回转半径可以用来定义这个被表示为物体的特定点所行进的典型距离。

回转半径的公式是什么？

用回转半径表示转动惯量的公式如下所示

I = mk² ……… (公式 1)

在这种情况下，I 是特定物体的转动惯量，m 与物体的质量相关联

因此，根据此方法，回转半径表示如下。

K = √I/m …….. (公式 2)

回转半径的单位是毫米。正如 Alsaker 等人（2019）所述，通过获得回转半径，个人可以找到刚体的转动惯量。为了更好地理解，对部分公式进行了演示。

如果一个物体有 n 个质量为 m 的粒子，则旋转轴前的垂直距离用 r₁、r₂、r₃… r_n 表示。现在我们知道，回转半径的转动惯量可以从公式 1 中得到。在那里，通过替换，我们可以得到，

I = m₁r₁² +  m₂r₂²+ m₃r₃³…… +  m_nr_n².......... (公式 3)

如果所有粒子的质量都相同，则

I  =  { mn(r₁² + r₂²+ r₃³ + ........+ r_n² ) }/n

我们可以进一步将 mn 写成“M”

从那里我们可以得到，

MK² = M { (r₁² + r₂²  + r₃³ +................ + r_n²)/n }

或 K = √ (r₁² + r₂²+ r₃³  +........................+  r_n²)/n

因此，可以得出结论，回转半径也可以表示为特定物体相对于其特定“旋转轴”的多个粒子的均方根距离。

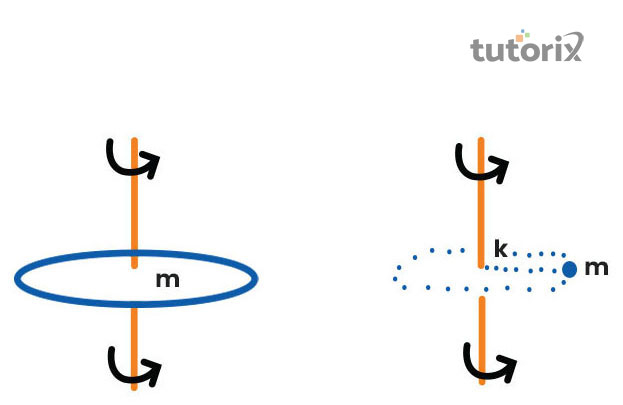
图 2：回转半径

回转半径在现实生活中的应用是什么？

回转半径可用于比较不同形状的几种结构在沿特定轴线受压时的行为。这可用于预测压缩梁的膨胀过程

回转半径的概念也用于地理数据分析。根据 Gurnev 等人（2020）的说法，它用于计算各种统计数据，包括各种地理位置的分布。它也用于聚合物物理学，用于定义聚合物链的尺寸。

结论

回转半径在结构分析的各个分支中都有多种实际应用。回转半径的概念有助于确定物体的旋转轴周围的转动惯量，该转动惯量等于物体的实际质量分布。它与某一点的径向距离相关联。但是，需要满足某些条件，即如果物体的总质量集中在该区域，则转动惯量可以与物体的实际质量分布相同。

常见问题

Q1. 回转半径的重要性是什么？

回转半径可用于确定梁或压力的堆积情况。此外，它在横截面积之间的强度分配中也很重要。回旋半径的较小估计值反映了截面处的旋转轴，在初步研究中很重要。

Q2. 回转半径在结构中的用途是什么？

回转半径估计了柱的刚度，如果二维回转半径的主惯性矩不相等，则柱将倾向于围绕与其较小的主惯性矩相关的特定轴发生屈曲。

Q3. 影响回旋半径的因素有哪些？

元件的某些部分会影响回转半径的估计。这些因素包括特定物体的尺寸和状态。旋转轴的布置和物体的位置以及其他因素取决于与物体旋转轴相关的质量分配。

Q4. 回转半径的 SI 单位是什么？

回转半径的 SI 单位可以用毫米或厘米或英寸来定义。它与惯性矩除以物体面积的平方根相关联。

Q5. 回转的公式是什么？

k = √IM (1) (1) k = I M 是回转的公式，其中回转半径绕旋转轴的测量利用质量惯性矩。

参考文献

期刊

Alsaker, C., Breidt, F. J., & van der Woerd, M. J. (2019)。小角 X 射线散射实验中回转半径的最小均方误差估计。美国统计协会杂志，114(525)，39-47。检索自：https://www.tandfonline.com

Gurnev, P. A., Stanley, C. B., Aksoyoglu, M. A., Hong, K., Parsegian, V. A., & Bezrukov, S. M. (2017)。半稀溶液中的聚乙二醇：本体中的回转半径和纳米孔中的分配。大分子，50(6)，2477-2483。检索自：https://www.ncbi.nlm.nih.gov

Haydukivska, K., Blavatska, V., & Paturej, J. (2020)。具有复杂结构的高斯聚合物的通用尺寸比率：回转半径与流体力学半径。科学报告，10(1)，1-11。检索自：https://www.nature.com/articles/s41598-020-70649-z

Khatiwada, P. (2020)。不规则建筑物的质心和回转半径的确定及其在扭转分析中的应用。国际工程技术研究杂志，7，1-7。检索自：https://www.researchgate.net

Shaheen, M. E., Ghazy, A. R., Kenawy, E. R., & El-Mekawy, F. (2018)。激光散射在壳聚糖分子量、第二维里系数和回转半径测定中的应用。聚合物，158，18-24。检索自：https://www.sciencedirect.com/science/article/pii/S0032386118309716

网站

Mechcontent，2022。关于回转半径。检索自：https://mechcontent.com/radius-of-gyration [检索日期：2022年6月10日]