第 0 节

---

引言

三角学的概念是由希腊数学家希帕克斯发展起来的，而“三角学”这个名称则是 16 世纪拉丁语的衍生词。

三角学是数学中最重要的分支之一。“三角学”这个名称由“Trigonon”和“Metron”这两个词组成，分别表示三角形和测量。它是研究直角三角形边与角之间关系的学科。在直角三角形中，斜边长度与邻边（底边）长度的比值称为一个角的正割。正割 0 度的角位于正 x 轴上。因此，正割 0 度的值 = 1。

在本教程中，我们将讨论正割 0 的值和三角学。

三角函数

三角学是数学的一个分支，研究直角三角形边与角的比值之间的关系。用于研究这种关系的比值称为三角比。三角函数的主要分支是正切、正弦和余弦角。主要函数还可以生成另外三个函数：余切、正割和余割函数。

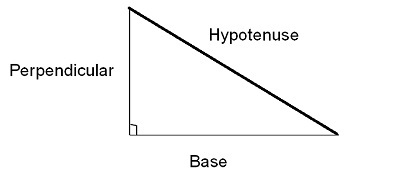
正弦函数

斜边长度与对边长度（垂直边）的比值称为角的正弦函数。根据上图中的三角形，sin 的值为

$$\mathrm{\sin\theta\:=\:\frac{垂直边}{斜边}}$$

余弦函数

它是斜边长度与邻边长度（底边）的比值。根据上面提到的三角形，余弦函数推导如下

$$\mathrm{\cos\theta\:=\:\frac{底边}{斜边}}$$

正切函数

邻边和对边的长度之比称为正切函数。

$$\mathrm{\tan\theta\:=\:\frac{垂直边}{底边}}$$

另外三个函数是从正弦、余弦和正切基本函数推导出来的，分别是正割、余割和余切。

$$\mathrm{\cot\theta\:=\:\frac{1}{\tan\theta}\:=\:\frac{底边}{垂直边}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$$

$$\mathrm{\:cosec\theta\:=\:\frac{1}{\sin\theta}\:=\:\frac{斜边}{垂直边}}$$

正割函数及其图形

在三角学中，正割函数是周期性的。在直角三角形中，斜边长度与底边长度的比值称为正割函数或 sec 函数。它也可以写成

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$$

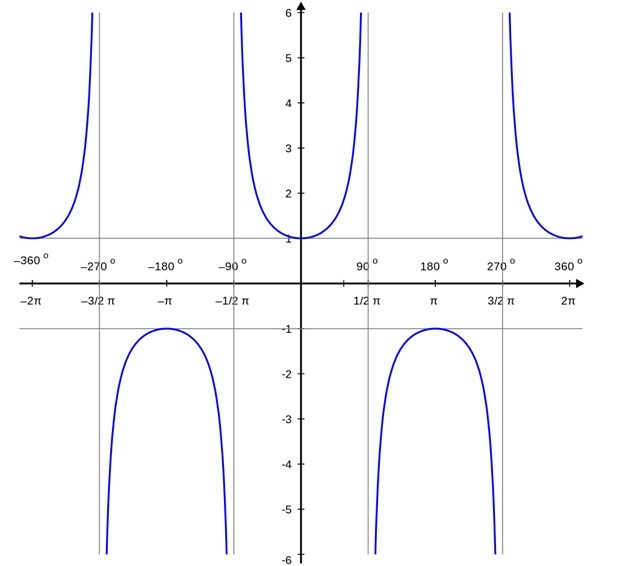
因为它余弦函数的倒数。由于我们已经熟悉余弦图，因此绘制正割图变得非常简单。通过确定每个余弦值的倒数，我们可以快速创建 $\mathrm{\sec\:x}$ 的图形。当 $\mathrm{\cos\:x}$ 的值非常小时，sec x 将具有非常大的值。具体来说，确定每个 $\mathrm{y\:=\:\cos\:x}$ 线上 y 值的 1/y。下表显示了一些以弧度表示的角度 -

x	cos x	sec x
0	1	1
$\mathrm{\frac{\pi}{6}}$	$\mathrm{\frac{\sqrt{3}}{2}}$	$\mathrm{\frac{2}{\sqrt{3}}}$
$\mathrm{\frac{\pi}{4}}$	$\mathrm{\frac{1}{\sqrt{2}}}$	$\mathrm{\sqrt{2}}$
$\mathrm{\frac{\pi}{3}}$	$\mathrm{\frac{1}{2}}$	2
$\mathrm{\frac{\pi}{2}}$	0	未定义

此外，我们注意到当余弦函数的值为零时，正割函数趋于无穷大，这意味着正割在该点未定义。因此，我们得到如下 sec x 图 -

第 0 节

正割 0 度的值为 1。正割 0 度表示为 $\mathrm{\sec\:(0°\:\times\:\frac{\pi}{180°})}$，通常称为 $\mathrm{\sec\:(0\pi)}$ 或 $\mathrm{\sec\:(0)}$。0 度的角位于正 x 轴上。因此，$\mathrm{\sec\:0°\:value\:=\:1}$。

$\mathrm{\sec\:(0°)}$ 可以表示为 $\mathrm{(\sec\:0°\:+\:n\:\times\:360°)}$, 𝑛 ∈ 𝑍。由于正割函数是周期函数，因此 $\mathrm{\sec\:0°\:=\:\sec\:360°\:=\sec\:720°}$，依此类推。

因为正割是偶函数，所以 $\mathrm{\sec\:(-0°)}$ 等于 $\mathrm{\sec\:(0°)}$，等于 1

正割函数的重要性

正割函数是三角学中重要的三角函数之一。一条直线或射线与曲线（特别是圆）相切不止一次，则它等价于直角三角形中斜边与底边的比值。正割函数的另一个名称是余弦函数的倒数。

例题

例 1 - 在下图中找到 secB 的值

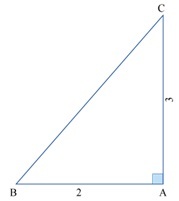
解 - 在三角形 ABC 中，边 AB 和 AC 的长度分别为 3 和 3，根据勾股定理，我们得到 BC 的长度为 $\mathrm{\sqrt{13}}$

我们知道，在直角三角形中，斜边长度与底边长度的比值称为正割函数或 sec 函数，即

$$\mathrm{\sec\:B\:=\:\frac{斜边}{底边}}$$

现在代入值，$\mathrm{\sec\:B\:=\:\frac{\sqrt{13}}{2}}$

例 2 - 找出 $\mathrm{\cos\:2\theta\:and\:\sec\:\theta\:}$ 之间的关系。

解 - 我们知道 $\mathrm{\cos\:2\theta\:=\:cos^{2}\theta\:-\:sin^{2}\theta\:}$ 且 $\mathrm{\sin^{2}\theta\:+\:\cos^{2}\:\theta\:=\:1}$

$\mathrm{\:\:\:\Rightarrow\:sin^{2}\theta\:=\:1\:-\:\cos^{2}\:\theta\;}$

现在将此值代入上式

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:\cos^{2}\theta\:-\:(1\:-\:\cos^{2}\theta\:)}$

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:2\cos^{2}\theta\:-\:1}$

我们知道 $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta\:}}$ 将此值代入上式。

$\mathrm{\:\:\:\:\:\:\cos\:2\theta\:=\:\frac{2}{\sec^{2}\:\theta}\:-\:1}$

例 3 - 求 $\mathrm{\tan\:45°\:+\:\cot\:45°}$ 的值

解 - $\mathrm{\tan\:45°\:+\:\cot\:45°}$

现在代入其值 $\mathrm{\tan\:45°\:+\:\cot\:45°\:=\:1\:+\:1}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:2}$

例 4 - 求 $\mathrm{\sin^{2}48°\:+\:\cos^{2}48°}$ 的值

解 - 给定方程为 $\mathrm{\sin^{2}48°\:+\:\cos^{2}48°}$

这里我们不需要代入其值，因为我们知道 $\mathrm{\sin^{2}\theta\:+\:cos^{2}\theta\:=\:1}$，其中 𝜃 可以是任何值，因此

$\mathrm{\sin^{2}48°\:+\:\cos^{2}48°\:=\:1}$

例 5 - 正割函数的定义域是什么？

解 - 正割函数的定义域为 $\mathrm{R\:-\:(2n\:+\:1)\frac{\pi}{2}}$，其中 R 为实数。

例 6 - 正割函数的值域是什么？

解 - 正割函数的值域为 $\mathrm{(-\infty,\:-1]\cup[+1\:,+\infty)}$

例 7 - 当 $\mathrm{\sec\:\theta}$ 的值为 2 时，求 $\mathrm{\tan\:\theta}$ 的值。

解 - 我们知道 $\mathrm{\tan\:\theta}$ 和 $\mathrm{\sec\:\theta}$ 之间的关系为

$$\mathrm{\sec^{2}\:\theta\:=\:1\:+\:\tan^{2}\:\theta}$$

$$\mathrm{\Rightarrow\:\tan^{2}\:\theta\:=\sec^{2}\:\theta\:-\:1}$$

已知 $\mathrm{\sec\theta}$ 的值，现在将此值代入上式，

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:2^{2}\:-\:1}$$

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:4\:-\:1}$$

$$\mathrm{\Rightarrow\:\tan^{2}\theta\:=\:3}$$

$$\mathrm{\tan\theta\:=\:\sqrt{3}}$$

例 8 - 使用正割函数求 secA 的值

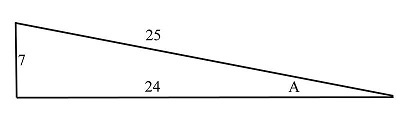
解 - 在此图中，底边、高和斜边的值分别为 24、7 和 25。

我们知道 $\mathrm{\sec\:A\:=\:\frac{25}{24}}$

例 9 - 当 $\mathrm{\sec\:\theta\:=\:2}$ 时，求 $\mathrm{\cos\:\theta}$ 的值

解 - 我们知道 $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{斜边}{底边}\:=\:\frac{斜边}{底边}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:cos\:\theta\:=\:\frac{1}{\sec\:\theta}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:cos\:\theta\:=\:\frac{1}{2}}$

结论

0 度角的正割三角函数值（正割 0 度）为 1。在直角三角形中，斜边长度与底边长度的比值称为正割函数或 sec 函数。它也可以写成

$\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{斜边}{底边}}$，因为它余弦函数的倒数。

常见问题

1. 三角学是什么意思？

三角学是数学的一个分支，研究直角三角形边与角的比值之间的关系。

2. sec 函数是什么意思？

在三角学中，正割函数是周期性的。在直角三角形中，斜边长度与底边长度的比值称为正割函数或 sec 函数

3. cos 和 sec 函数之间有什么关系？

正割函数也写作 $\mathrm{\sec\:\theta\:=\:\frac{1}{\cos\:\theta}\:=\:\frac{斜边}{邻边}}$，因为它余弦函数的倒数。

4. 正割函数在 0 度时的值是多少？

0 度角的正割三角函数值（Sec 0 度）为 1。

5. 求正割函数的奇偶性？

正割函数是偶函数，因为对于所有 x，$\mathrm{\sec(-x)\:=\:\sec\:x}$