Sec 60

---

引言

三角学是数学的一个分支，研究直角三角形的边与角之间的关系。用于研究这种关系的比率称为三角比率。即正弦、余弦、正切、余切、正割、余割。直角三角形的三个边分别是斜边、底边（邻边）和高（对边），几何中的三角比由此得出。

“三角学”这个名称是由“Trigonon”和“Metron”这两个词组成的，分别表示三角形和测量。在直角三角形中，斜边长度与邻边（底边）长度的比值称为一个角的正割。在本教程中，我们将讨论 sec60 度的值和三角学。

三角函数

三角函数的主要分支是正切、正弦和余弦角。此外，可以使用主要函数生成另外三个函数：余切、正割和余割。与主要三角函数相比，另外三个函数通常使用得更频繁。有关这三个主要函数的说明，请参见附图。三角学通常定义为直角三角形。

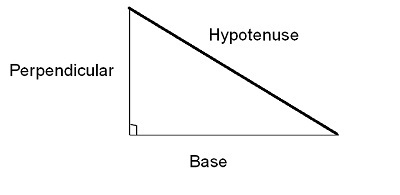
正弦函数

斜边长度与对边长度（高）之比称为角度正弦函数。上面三角形的正弦值如下：

$$\mathrm{\sin\theta\:=\:\frac{高}{斜边}}$$

余弦函数

它是斜边长度与邻边长度（底边）之比。从上面提到的三角形中，余弦函数推导如下：

$$\mathrm{\cos\theta\:=\:\frac{底边}{斜边}}$$

正切函数

邻边和对边的长度之比称为正切函数。

$$\mathrm{\tan\theta\:=\:\frac{高}{底边}}$$

另外三个函数是从正弦、余弦和正切基本函数推导出来的，分别是正割、余割和余切。

$$\mathrm{\cot\theta\:=\:\frac{1}{\tan\theta}\:=\:\frac{底边}{高}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$$

$$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$$

三角方程或恒等式是适用于直角三角形的方程。以下是一些特殊的三角公式：

勾股恒等式

$$\mathrm{\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$$

$$\mathrm{\tan^{2}\:\theta\:+\:1\:=\:\sec^{2}\:\theta}$$

$$\mathrm{\cot^{2}\:\theta\:+\:1\:=\:cosec^{2}\:\theta}$$

$$\mathrm{\sin\:2\theta\:=\:2\sin\:\theta\:\cos\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\cos^{2}\theta\:-\:\sin^{2}\:\theta}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{2\:\tan\:\theta}{1\:-\:\tan^{2}\:\theta}}$$

$$\mathrm{\cos\:2\theta\:=\:\frac{\cot^{2}\:\theta\:-\:1}{2\:\cot\:\theta}}$$

和差恒等式

角度 u 和 v 有如下关系：

$$\mathrm{\sin(u\:+\:v)\:=\:\sin(u)\:\cos(v)\:+\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:+\:v)\:=\:\cos(u)\:\cos(v)\:-\:sin(u)\sin(v)}$$

$$\mathrm{\sin(u\:-\:v)\:=\:\sin(u)\:\cos(v)\:-\:cos(u)\sin(v)}$$

$$\mathrm{\cos(u\:-\:v)\:=\:\cos(u)\:\cos(v)\:+\:sin(u)\sin(v)}$$

$$\mathrm{\tan(u\:+\:v)\:=\:\frac{\tan(u)\:+\:\tan(v)}{1\:-\:\tan(u)\:\tan(v)}}$$

$$\mathrm{\tan(u\:-\:v)\:=\:\frac{\tan(u)\:-\:\tan(v)}{1\:+\:\tan(u)\:\tan(v)}}$$

正割函数及其图像

在三角学中，正割函数是周期函数。在直角三角形中，斜边长度与底边长度之比称为正割函数或 sec 函数。它也写成 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$，因为它是的倒数。

因为它是余弦函数的倒数。由于我们已经熟悉余弦曲线，所以绘制正割曲线变得非常简单。通过确定每个余弦值的倒数，我们可以快速创建 sec x 的图形。当 cos x 的值很小时，sec x 的值将非常大。具体来说，确定 $\mathrm{\frac{1}{y}}$ 对于直线 $\mathrm{y\:=\:cosx}$ 上的每个 y 值。下表显示了一些以弧度表示的角度

x	$\mathrm{\cos\:x}$	$\mathrm{\sec\:x}$
0	1	1
$\mathrm{\frac{\pi}{6}}$	$\mathrm{\frac{\sqrt{3}}{2}}$	$\mathrm{\frac{2}{\sqrt{3}}}$
$\mathrm{\frac{\pi}{4}}$	$\mathrm{\frac{1}{\sqrt{2}}}$	$\mathrm{\sqrt{2}}$
$\mathrm{\frac{\pi}{3}}$	$\mathrm{\frac{1}{2}}$	2
$\mathrm{\frac{\pi}{2}}$	0	未定义

此外，我们注意到，当余弦函数的值为零时，正割函数趋于无穷大，这意味着正割函数在该点未定义。因此，我们得到 sec x 图如下：

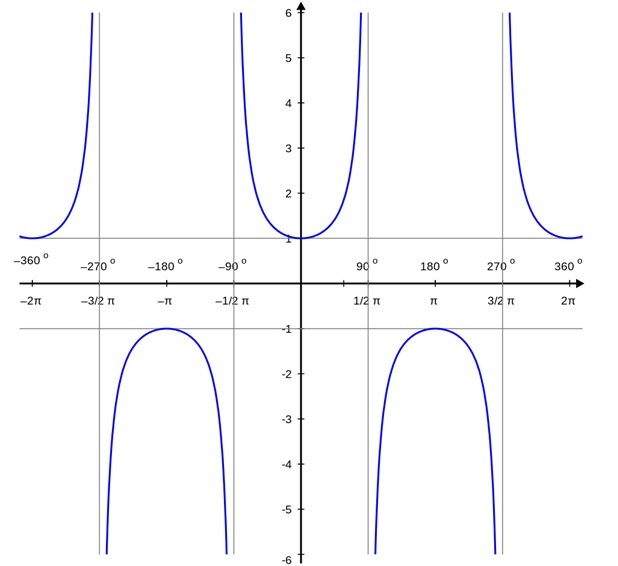
Sec 60

所以，sec 60 度的值为 2。sec 60 度用弧度表示。sec 60 度的 60° 角位于 0° 和 90°（第一象限）之间。sec 60° 值 = 2，因为正割函数在第一象限为正。

鉴于正割函数是一个周期函数，sec 60° 可以表示为

注意 - 正割是一个偶函数，$\mathrm{\sec(-60°)\:等于\:\sec(60°)}$

正割函数的重要性

正割函数是三角学中重要的三角函数之一。一条直线或射线与曲线（特别是圆）相切一次以上，则它等同于直角三角形的斜边与底边的比值。正割函数的另一个名称是余弦函数的倒数

例题

例1 - 当 $\mathrm{\sec\:\theta}$ 的值为 2 时，求 𝑡𝑎𝑛 𝜃 的值。

解 - 我们知道 $\mathrm{\tan\:\theta}$ 和 $\mathrm{\sec\:\theta}$ 之间的关系是

$$\mathrm{\sec^{2}\:\theta\:=\:1\:+\:tan^{2}\:\theta}$$

$$\mathrm{\tan^{2}\:\theta\:=\:\sec^{2}\:\theta\:-\:1}$$

已知 $\mathrm{\sec\:\theta}$ 的值为 2，现在将此值代入上述方程：

$$\mathrm{\tan^{2}\:\theta\:=\:2^{2}\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:4\:-\:1}$$

$$\mathrm{\tan^{2}\:\theta\:=\:3}$$

$$\mathrm{\tan\:\theta\:=\:\sqrt{3}}$$

例2 - 当 𝑠𝑒𝑐𝜃 的值为 1 时，求 𝑡𝑎𝑛𝜃 的值。

解 - 已知 $\mathrm{\sec\:\theta\:=\:1}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\theta\:=\:0°}$

所以，$\mathrm{\tan\:\theta\:=\:\tan0°\:=\:0}$

例3 - 当 𝑠𝑒𝑐𝜃 的值为 1 时，求 𝑐𝑜𝑠 𝜃 的值。

解 - 我们知道 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{\sec\:\theta}}$

$\mathrm{\:\:正割函数的重要性\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\cos\:\theta\:=\:\frac{1}{1}\:=\:1}$

例4 - 正割函数的定义域是什么？

解 - 正割函数的定义域是 $\mathrm{R\:-\:(2n\:+\:1)\:\frac{\pi}{2}}$，其中 R 为实数。

例5 - 求 $\mathrm{\cos\:2\theta\:和\:\sec\:\theta}$ 之间的关系

解 - 我们知道 $\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:\sin^{2}\:\theta}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sin^{2}\:\theta\:+\:\cos^{2}\:\theta\:=\:1}$

$\mathrm{\Rightarrow\:\sin^{2}\:\theta\:=\:1\:-\:\cos^{2}\:\theta}$

现在将此值代入上述方程

$\mathrm{\cos\:2\theta\:=\:cos^{2}\:\theta\:-\:(1\:-\:\cos^{2}\:\theta)}$

$\mathrm{\cos\:2\theta\:=\:2\cos^{2}\:\theta\:-\:1}$

我们知道 $\mathrm{\sec\:\theta\:=\frac{1}{\cos\:\theta}}$ 将此值代入上述方程

$\mathrm{\cos\:2\theta\:=\:\frac{2}{\sec^{2}\:\theta}\:-\:1}$

例6 - 求 $\mathrm{2\tan\:45°\:+\:\sec\:60°}$ 的值

解 - $\mathrm{2\tan\:45°\:+\:\sec\:60°}$

现在代入它们的值 $\mathrm{2\tan\:45°\:+\:\sec\:60°\:=\:2\:+\:2}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:4}$

例7 - 化简 $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

解 - 给定的方程是 $\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}}$

我们知道 $\mathrm{\tan\:45°}$ 的值为 1，𝑠𝑒𝑐60° 的值为 2

所以，$\mathrm{\frac{\sec^{2}\:60°\:+\:\tan\:45°}{2\tan\:45°}\:=\:\frac{4\:+\:1}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{5}{2}}$

例8 - 化简 $\mathrm{\sec60°\:-\:\cos60°}$

解 - 给定的方程是 $\mathrm{\sec60°\:-\:\cos60°}$

$\mathrm{\Rightarrow\:2\:-\:\frac{1}{2}}$

$\mathrm{\Rightarrow\:\frac{3}{2}}$

例9 - 化简 $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

解 - 给定的方程是 $\mathrm{\frac{\sec60°}{\cos60°}\:-\:\frac{\cos60°}{\sec60°}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{2}{\frac{1}{2}}\:-\:\frac{\frac{1}{2}}{2}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:4\:-\:\frac{1}{4}}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\frac{15}{4}}$

结论

60度角的正割三角函数值是2。在直角三角形中，斜边长度与底边长度之比称为正割函数或 sec 函数。它也写成 $\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$，因为它是的倒数

常见问题

1. 正割函数是什么意思？

在直角三角形中，斜边长度与底边长度之比称为正割函数或 sec 函数

2. 三角学是什么意思？

三角形的边长比与角度之间的关系是三角学这个数学分支的研究对象。

3. 60度时正割函数的值是多少？

60度角的正割三角函数值（Sec 60度）为2。

4. 求正割函数的奇偶性？

正割函数是偶函数，因为对于所有x，$\mathrm{\sec(-x)\:=\:\sec\:x}$。

5. 余弦函数和正割函数之间有什么关系？

正割函数也可以写成$\mathrm{\sec\theta\:=\:\frac{1}{\cos\theta}\:=\:\frac{斜边}{底边}}$，因为它是余弦函数的倒数。