1 到 25 的平方根

---

简介

1 到 25 的平方根是 1 到 25 所有数字的平方根列表。平方根可以具有不同类型的数值。1 到 25 的根的正整数数值范围从 1 到 5。对于非完全平方数，平方根是一个无理数。

任何数字 x 的根表示为 √𝑥（根式）和 $\mathrm{(x)^{2}}$（指数式）

平方根

任何数字的平方根是可以乘以自身得到原数字的值。平方根是平方数的逆运算。因此，平方和平方根是相关的概念。

如果 x 是 y 的平方根，则表示为 $\mathrm{x\:=\:\sqrt{y}}$。或者，您也可以将原始方程式写成 $\mathrm{x^{2}\:=\:\sqrt{y}}$。这里，“√”是用于表示数字平方根的符号（根式）。将一个数字乘以自身得到该数字的平方。有效范围内的平方数的平方根表示唯一的数字。

例如，三的平方是 9，$\mathrm{3^{2}\:=\:9}$，9 的平方根是 √ 9 = 3。由于 9 是一个完全平方数，因此您可以轻松找到平方根。但是对于 3、7、5 等非完全平方数，您必须使用其他方法来找到平方根。

1-25 平方根表

1-25 数字的平方根值的表格为

数字 (x)	数字的平方根 $\mathrm{(\sqrt{X})}$（四舍五入到小数点后 3 位）
1	1.000
2	1.414
3	1.732
4	2.000
5	2.236
6	2.449
7	2.646
8	2.828
9	3.000
10	3.162
11	3.317
12	3.464
13	3.606
14	3.742
15	3.873
16	4.000
17	4.123
18	4.243
19	4.359
20	4.472
21	4.583
22	4.690
23	4.796
24	4.899
25	5.000

求平方根的方法

• 方法 1 - 素因数分解

示例 - $\mathrm{\sqrt{25}}$

25 的素因数分解是 $\mathrm{5\times\:5}$

出现两次的数字 - 5

因此，$\mathrm{\sqrt{25}\:=\:5}$

• 方法 2 - 长除法

因式分解

完全平方数的平方根可以使用上面详细讨论的因式分解方法轻松计算。让我们在这里澄清一些示例 -

数字	素因数分解	平方根
16	$\mathrm{2\times\:2\times\:2\times\:2}$	$\mathrm{\sqrt{16}\:=\:2\times\:2\:=\:4}$
144	$\mathrm{2\times\:2\times\:2\times\:2\times\:3\times\:3}$	$\mathrm{\sqrt{144}\:=\:2\times\:2\times\:3\:=\:12}$
169	$\mathrm{13\times\:13}$	$\mathrm{\sqrt{169}\:=\:13}$
256	$\mathrm{256\:=\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:2}$	$\mathrm{\sqrt{256}\:=\:(2\times\:2\times\:2\times\:2)\:=\:16}$
576	$\mathrm{576\:=\:2\times\:2\times\:2\times\:2\times\:2\times\:2\times\:3\times\:3}$	$\mathrm{\sqrt{576}\:=\:2\times\:2\times\:2\times\:3\:=\:24}$

估计

此方法用作近似值来猜测数值并找到平方根。

例如，4 的平方根是 2，9 的平方根是 3，因此我们可以推断 5 的平方根介于 2 和 3 之间

但是您需要查看 $\mathrm{\sqrt{5}}$ 的数值是接近 2 还是 3。

让我们检查 2.2 和 2.8 的平方。

$\mathrm{2.2\:=\:4.84}$

$\mathrm{2.8\:=\:7.84}$

由于 2.2 的平方根更接近 5，因此我们可以估计 5 的平方根约等于 2.2

长除法

求非完全平方数的平方根有点困难，但是可以使用称为长除法的方法计算。这可以通过下面的示例来理解

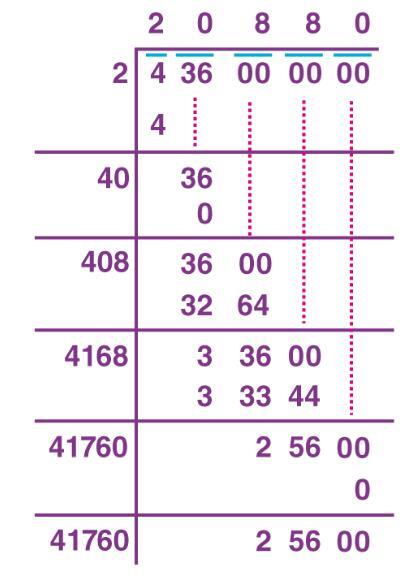
已解决示例

1)正方形金属板的面积为 18 平方英寸。求该金属板一边的尺寸。

答案 -

设金属板的一边尺寸为“a”

正方形金属板面积 $\mathrm{=\:18\:in^{2}\:=\:a^{2}}$

$$\mathrm{即\:a^{2}\:=\:18}$$

$$\mathrm{a\:=\:\sqrt{18}\:=\:4.243\:in}$$

因此，金属板边长为 4.243 英寸

2)一个圆形桌面，面积为 19π 平方英寸。求桌面的半径（以英寸为单位）？

答案 -

圆形桌面面积 $\mathrm{=\:19\pi\:in^{2}\:=\:\pi\:r^{2}}$

即 $\mathrm{19\:=\:r^{2}}$ 2。因此，使用半径中的数值 $\mathrm{=\:\sqrt{19}}$

桌面半径 = 4.359 英寸。

3) 求 $\mathrm{6\sqrt{7}\:+\:3\sqrt{7}}$ 的值

答案 -

$\mathrm{6\sqrt{7}\:+\:3\sqrt{7}\:=\:6\times\:(2.646)\:+\:3\:\times\:(2.646)\:=\:9\:\times\:2.646[√7的值为\:2.646]}$

因此 $\mathrm{6\sqrt{7}\:+\:3\sqrt{7}\:=\:9\:\times\:2.646\:=\:23.814}$

结论

在本教程中，我们学习了平方和平方根，主要是 1 到 25 的整数平方根。如果一个数字的范围具有完全平方数，则该范围内存在完全平方根。如果数字以偶数个零 (0) 结尾，则它可以有平方根。

您可以将两个平方根的数值相乘。例如，将 $\mathrm{\sqrt{3}}$ 乘以 $\mathrm{\sqrt{2}}$ 会得到 $\mathrm{\sqrt{6}}$。将两个相等的平方根相乘，最终结果是初始数字。这意味着结果不再是平方根。例如，将 $\mathrm{\sqrt{7}}$ 乘以 $\mathrm{\sqrt{7}}$ 会得到 7。无理数的平方根是无理数。完全平方数不能为负数。

常见问题解答

1. 1 到 25 的平方根的值是多少？

1 到 25 的平方根值是数字 𝑥，当它乘以自身时会得到原数字。

它可以具有不同类型的数值（正数、负数）。在 1 和 25 之间，1、4、9、16 和 25 的平方根是整数（有理数），而 2、3、5、6、7、8、10、11、12、13、14、15、17、18、19、20、21、22、23 和 24 的平方根是（无理）小数，这些小数不会停止或重复。

2. 如何计算 1 到 25 的平方根？

通常有两种方法可以计算 1 到 25 的平方根值。素因数分解可用于完全平方数（1、4、9、16 和 25），对于非完全平方数（2、3、5、6、7、8、10、11、12、13、14、15、17、18、19、20、21、22、23、24），您可以使用长除法方法

3. 1 到 25 中哪些数字的平方根介于 2 和 3 之间？

1 到 25 的平方根数值介于 2 和 3 之间的是 $\mathrm{\sqrt{4}(2)\:,\:\sqrt{5}(2.236)\:,\:\sqrt{6}(2.449)\:,\:\sqrt{7}(2.646)\:,\:\sqrt{8}(2.828)\:,\:\sqrt{9}(3)}$

4. 25 的平方根的值是多少？

$\mathrm{\sqrt{25}\:的值是\:5}$

5. 1 到 25 的平方根范围是有理数吗？

数字 1、4、9、16 和 25 是完全平方数，因此它们的平方根是整数。因此，它们可以用 $\mathrm{\frac{p}{q}}$ 的形式表示，其中 p 和 q 是互质整数，且 $\mathrm{q\neq\:0}$。