信号类型 – 矩形、三角形、符号、Sinc 和高斯函数

---

一个或多个自变量的单值函数，包含某些信息，称为信号。

基本信号类型

有几种基本信号在信号与系统研究中起着重要作用。这些基本信号是构建更复杂信号的基本构建块。这些基本信号也称为标准信号。

矩形信号

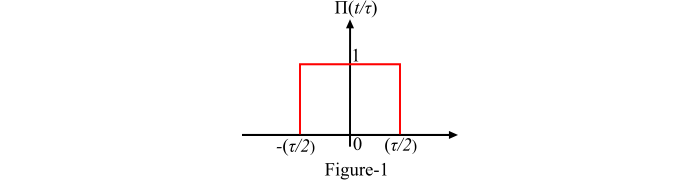
产生宽度为 τ（其中 τ = 1 表示单位矩形函数）并以 t = 0 为中心的矩形脉冲的信号称为矩形信号。矩形信号脉冲的高度也为 1。数学上，单位矩形信号定义为：

$$\mathrm{\prod \left ( \frac{t}{\tau} \right )=\left\{\begin{matrix} 1\: 当\: \left | t \right |\leq \left ( \frac{\tau }{2} \right )\ 0\; 其他情况\ \end{matrix}\right.}$$

矩形信号也称为单位脉冲、门函数或归一化矩形函数。此外，矩形函数是时间的偶函数。矩形脉冲信号的图形表示如图 1 所示。

Explore our latest online courses and learn new skills at your own pace. Enroll and become a certified expert to boost your career.

三角形信号

图形呈三角形的函数称为三角形信号。三角形信号也称为帽函数或帐篷函数。数学上，单位三角脉冲信号 Δ(t/τ) 定义为：

$$\mathrm{\Delta\left ( \frac{t}{\tau} \right )=\left\{\begin{matrix} 1-\left ( \frac{2\left | t \right |}{\tau } \right )\; 当\left | t \right |< \left ( \frac{\tau }{2} \right )\ 0\; 当\left | t \right |> \left ( \frac{\tau}{2} \right )\ \end{matrix}\right.}$$

三角形信号也是时间的偶函数。三角形信号的图形表示如图 2 所示。

符号函数

符号函数是一个奇数学函数，它提取实数的符号。符号函数表示为 sgn。数学上，单位符号函数定义为：

$$\mathrm{sgn(t)=\left\{\begin{matrix} 1\; 当\: t> 0\ -1\; 当\: t< 0\ \end{matrix}\right.}$$

单位符号函数的图形表示如图 3 所示。

符号函数也可以用单位阶跃函数表示如下：

sgn(t) = -1 + 2u(t)

Sinc 函数

Sinc 函数定义为：

$$\mathrm{sinc(t)=\frac{\sin t}{t}\: 当 -\infty< t<\infty}$$

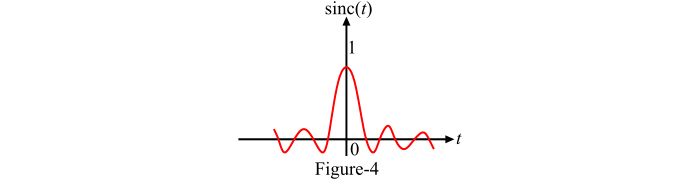
根据定义，很明显 sinc 函数以 2π 为周期振荡，并随着时间 (t) 的增加而衰减。sinc 函数在 t = nπ 处的值为零，其中 n = ±1，±2，±3… sinc 函数也是时间的偶函数。

单位 sinc 函数的图形表示如图 4 所示。

高斯函数

高斯函数在概率论中非常有用。高斯函数定义为：

g_a(t) = e^-at2 当 − ∞ < t < ∞

单位高斯函数的图形表示如图 5 所示。