
单位分数边长的立方体组成的立体体积
引言
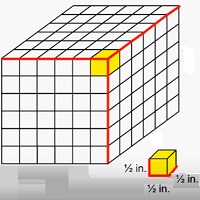
在这里,我们求解由单位分数边长的立方体组成的立体的体积。例如,考虑一个尺寸为3英寸×3英寸×3英寸的立体,它由边长为$\frac{1}{2}$英寸的小立方体组成。
在这种情况下,该立体由6×6×6个边长为$\frac{1}{2}$英寸的小立方体组成。因此,在这种情况下,立体的体积为:
体积 = 长×宽×高 = $6 \times \frac{1}{2} \times 6 \times \frac{1}{2} \times 6 \times \frac{1}{2}$
= 3 × 3 × 3 = 27立方英寸
由单位分数边长的立方体组成的立体的体积公式
假设该立体是一个边长为a单位的立方体
b = 每条边上单位分数边长的立方体的数量
k = 单位分数边长
立体的体积 = b × k × b × k × b × k 立方单位
例1
求以下由单位分数边长的立方体组成的立体的体积。每个棱柱单位用厘米表示(不成比例)
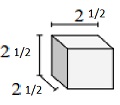
解
步骤1
单位分数边长为$\frac{1}{2}$厘米的立方体立体
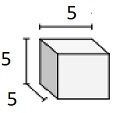
步骤2
体积 V = 长×宽×高 = $2 \frac{1}{2} \times 2 \frac{1}{2} \times 2 \frac{1}{2}$
= $5 \times \frac{1}{2} \times 5 \times \frac{1}{2} \times 5 \times \frac{1}{2}$
= $15 \frac{5}{8}$ 立方厘米
例2
求以下由单位分数边长的立方体组成的立体的体积。每个棱柱单位用厘米表示(不成比例)
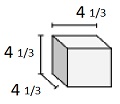
解
步骤1
单位分数边长为$\frac{1}{3}$厘米的立方体立体
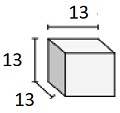
步骤2
体积 V = 长×宽×高 = $4 \frac{1}{3} \times 4 \frac{1}{3} \times 4 \frac{1}{3}$
= $13 \times \frac{1}{3} \times 13 \times \frac{1}{3} \times 13 \times \frac{1}{3}$
= $81 \frac{10}{27}$ 立方厘米