数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
"
解：求出每个给定平行四边形的面积。解：$(a)$. 平行四边形的面积$=底\times高$$=7\ cm\times4\ cm$$=28\ cm^2$$(b)$. 平行四边形的面积$=底\times高$$=5\ cm\times3\ cm$$=15\ cm^2$$(c)$. 平行四边形的面积$=底\times高$$=2.5\ cm\times3.5\ cm$ $=8.75\ cm^2$$(d)$. 平行四边形的面积$=底\times高$$=5\ cm\times4.8\ cm$$=24\ cm^2$ $(e)$. 平行四边形的面积$=底\times高$$=2\ cm\times4.4\ cm$$=8.8\ cm^2$
$(a)$. 三角形的面积 $= 87\ cm^2$底 $= 15\ cm$三角形的面积 $= \frac{1}{2}\times 底\times 高$$87\ cm^2 = \frac{1}{2}\times 15\ cm\times 高$高 $= \frac{87\ cm^2\times 2}{15\ cm}$高 $= \frac{174\ cm^2}{15\ cm}$高 $= 11.6\ cm$$(b)$. 三角形的面积 $= 1256\ mm^2$高 $= 31.4\ mm$三角形的面积 $= \frac{1}{2}\times 底× 高$$1256\ mm^2 = \frac{1}{2}\times 底\times 31.4\ mm$底 $= \frac{(2\times 1256\ mm^2)}{31.4\ mm}$底 $=\frac{2512\ mm^2}{31.4\ mm}$底 $= 80\ mm$$(c)$. 三角形的面积 $= 170.5\ cm^2$底 $= 22\ cm$三角形的面积 $= \frac{1}{2}\times 底× 高$$170.5\ cm^2 = \frac{1}{2}\times 22\ cm\times 高$高 $= \frac{(2\times 170.5\ cm^2)}{22\ cm}$高 $= \frac{341\ cm^2}{22\ cm}$高 $= 15.5\ cm$
"
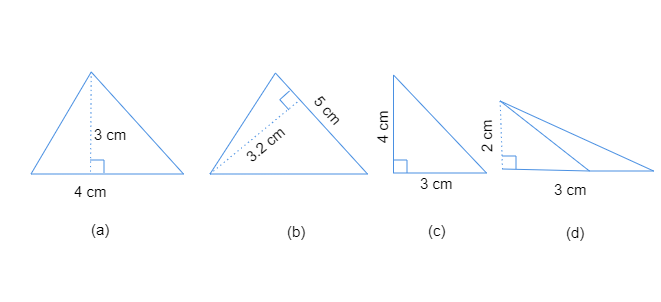
解：求出每个给定三角形的面积。解：$(a)$. 三角形的面积$=\frac{1}{2}\times 底\times 高$ $=\frac{1}{2}\times4\ cm\times3\ cm$ $=6\ cm^2$$(b)$. 三角形的面积$=\frac{1}{2}\times 底\times 高$$\frac{1}{2}\times5\ cm\times3.2\ cm$$=8.0\ cm^2$$(c)$. 三角形的面积$=\frac{1}{2}\times 底\times 高$$=\frac{1}{2}\times3\ cm\times4\ cm$$=6\ cm^2$$(d)$ 三角形的面积$=\frac{1}{2}\times 底\times 高$$=\frac{1}{2}\times3\ cm\times2\ cm$$=3\ cm^2$
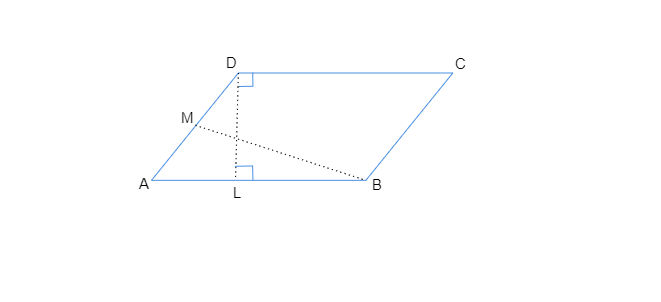
$(a)$. $SR = 12\ cm$ 且 $QM = 7.6\ cm$平行四边形 $PQRS$ 的面积 $= 底\times 高$$= SR\times QM$$= 12\ cm\times 7.6\ cm$$= 91.2 cm^2$$(b)$. 底 $= PS = 8\ cm$平行四边形的面积 $= 91.2\ cm^2$ [在 $(a)$ 部分计算得出]平行四边形 $PQRS$ 的面积 $= 底\times 高$$91.2\ cm^2 = 8 cm\times QN$$QN = 91.2\ cm^2 / 8 cm$$QN = 11.4\ cm$
已知：矩形的周长为 $130\ cm$。矩形的宽为 $30\ cm$。解：求出矩形的长和面积。解：如题所述，矩形的周长 $P=130\ cm$矩形的宽 $b=30\ cm$设“$l$”为矩形的长。我们知道，$P=2(l+b)$$\Rightarrow 130\ cm=2(l+30\ cm)$$\Rightarrow 130\ cm=2l+60\ cm$$\Rightarrow 2l=130-60$$\Rightarrow 2l=70$$\Rightarrow l=\frac{70}{2}$$\Rightarrow l=35\ cm$因此，矩形的面积 $A=l\times b$$=35\ cm\times 30\ cm$$=1050\ cm^2$因此，矩形的长为 $35\ cm$，矩形的面积为 $1050\ cm^2$。阅读更多
已知：一根铁丝围成一个矩形。它的长是 $40\ cm$，宽是 $22\ cm$。解：求出将相同的铁丝重新弯成正方形时每边的长度，并求出哪种形状围成的面积更大。解：如题所述，长 $l=40\ cm$ 宽 $b=22\ cm$矩形的面积 $A_{rectangle}=l\times b$$=40\ cm\times 22\ cm$$=880\ cm^2$我们知道矩形周长的公式 $P_{rectangle}=2(l+b)$或 $P_{rectangle}=2(40\ cm+22\ cm)$或 $P_{rectangle}=2(62\ cm)$或 $P_{rectangle}=124\ cm$设“$a$”为重新弯曲铁丝形成的正方形的边长。周长将保持不变。正方形的周长... 阅读更多
已知：一块矩形纸片的周长是 $100\ cm$。如果长是 $35\ cm$。解：求出它的宽和面积。解：如题所述，矩形的周长 $S=100\ cm$矩形纸片的长度 $l=35\ cm$设“$b$”为矩形纸片的宽。我们知道，$S=2(l+b)$$100\ cm=2(35\ cm+b)$$\Rightarrow 100=70+2b$$\Rightarrow 100-70=2b$$\Rightarrow 30=2b$$\Rightarrow b=\frac{30}{2}$$\Rightarrow b=15\ cm$因此，矩形纸片的宽为 $15\ cm$，矩形纸片的面积为 $525\ cm^2$。阅读更多
已知：一块矩形土地的面积是 $440\ m^2$，长是 $22\ m$。解：求出土地的宽和周长。解：如题所述，土地的长 $l=22\ m$ 土地的面积 $A=440\ m^2$设“$b$”为土地的宽。我们知道，土地的面积 $A=l\times b$ 或 $440\ m^2=22\ m\times b$ $\Rightarrow b=\frac{440}{22}$ $\Rightarrow b=20\ m$我们知道矩形周长的公式 $=2(l+b)$ $=2(22+20)$ $=2(42)$ $=84\ m$因此，矩形土地的宽为 $20\ m$，周长为... 阅读更多
已知：正方形的周长 $= 320 m$。解：求出正方形的面积。解：边长为 's' 的正方形的周长为 4s。$ 4a = 320 m$ (其中 a 是正方形的边长)$a = \frac{320}{4} m$$a = 80 m$现在，$$正方形的面积 = a^2$$正方形的面积 $= (80)^2 m^2$正方形的面积 $= 6400 m^2$。因此，正方形的面积是 $6400 m^2$。
"
已知：平行四边形的面积 $=1470\ cm^2$ $AB=35\ cm$ 且 $AD=49\ cm$解：求出 $BM$ 的长度。解：我们知道，底为 b、高为 h 的平行四边形的面积 $=b\times h$这意味着，$1470=49\times BM$$BM= \frac{1470}{49}\ cm$$BM=30\ cm$因此，BM 的长度是 30 cm。