数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理
化学
生物
数学
英语
经济学
心理学
社会学
服装学
法学
(a) 这种废水的俗称是污水。(b) 污水含有细菌、病毒、原生动物、真菌和寄生虫（蠕虫），这些可能会导致霍乱、伤寒和黄疸等疾病。(c) 饮用被这种废水污染的河水可能导致霍乱、伤寒、腹泻、痢疾和黄疸等疾病。
将第一栏中的项目与第二栏中的一个或多个项目匹配
| 第一栏 | 第二栏 |
| (i) 阻止光合作用 | (a) 排入河流的污水 |
| (ii) 破坏臭氧层 | (b) 田间过量施肥 |
| (iii) 产生酸雨 | (c) 空气中的二氧化碳 |
| (iv) 通过脱氧使鱼类死亡 | (d) 空气中的灰尘 |
| (v) 导致水传播疾病 | (e) 氯氟烃 (CFCs) |
| (vi) 导致全球变暖 | (j) 二氧化硫 |
第一栏 第二栏 (i) 阻止光合作用 (d) 空气中的灰尘 (ii) 破坏臭氧层 (e) 氯氟烃 (CFCs) (iii) 产生酸雨 (j) 二氧化硫 (iv) 通过脱氧使鱼类死亡 (b) 田间过量施肥 (v) 导致水传播疾病 (a) 排入河流的污水 (vi) 导致全球变暖 (c) 空气中的二氧化碳
化石燃料在空气中燃烧会产生二氧化硫和二氧化氮等气体。二氧化硫和二氧化氮与大气中的水蒸气反应形成硫酸和硝酸。这些酸与雨水结合使雨水酸化。这被称为酸雨。燃烧化石燃料造成的酸雨使湖水酸度过高，从而杀死鱼类。化肥充当藻类生长的养分。当这些藻类死亡时，它们又成为细菌等分解者的养分。在这个过程中，大量的……阅读更多
家庭中不完全燃烧木柴会产生一种剧毒气体 X，即一氧化碳。吸入后，一氧化碳会与血液中存在的物质 Y（血红蛋白）结合。一氧化碳与血液中的血红蛋白结合，降低血液的携氧能力，导致呼吸问题和窒息。因此，物质 Z 是氧气。
物质 P 是化肥。化肥充当藻类生长的养分。当这些藻类死亡时，它们又成为细菌等分解者的养分。在这个过程中，水中的大量氧气被消耗掉，导致水中缺氧。这可能会杀死水生生物。物质 Q 是藻类，R 是细菌，S 是氧气。
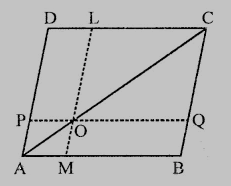
"\已知：$ABCD$ 是一个平行四边形。$O$ 是 $AC$ 上的任意一点。$PQ \parallel AB$ 且 $LM \parallel AD$。要求：我们必须证明 $ar(平行四边形 DLOP) = ar(平行四边形 BMOQ)$。解答：平行四边形的对角线将其分成两个面积相等的三角形。因此，$ar(\triangle ADC) = ar(\triangle ABC)$$ar(\triangle APO) + ar(\|gm DLOP) + ar(\triangle OLC) = ar(\triangle AOM) + ar(\|gm BMOQ) + ar( \triangle OQC)$.....…(i)$AO$ 和 $OC$ 分别是平行四边形 $AMOP$ 和 $OQCL$ 的对角线，这意味着 $ar(\triangle APO) = ar(\triangle AMO)$.....…(ii)$ar(\triangle OLC) = ar(\triangle OQC)$....…(iii)从 (i) 中减去 (ii) 和 (iii)，我们得到 $ar(\|gm DLOP) = ar(\|gm BMOQ)$。证毕。阅读更多
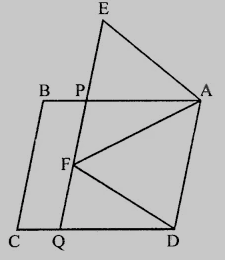
"\已知：$ABCD$ 和 $AEFD$ 是两个平行四边形。要求：我们必须证明 $PE = FQ$。解答：在 $\triangle AEP$ 和 $\triangle DFQ$ 中，$AE = DF$ (平行四边形的对边)$\angle AEP = \angle DFQ$ (同位角)$\angle APE = \angle DQF$ (同位角)因此，根据 AAS 公理，$\triangle AEP \cong \triangle DFQ$这意味着 $PE = QF$ (全等三角形的对应边)证毕。
已知：$D$ 是 $\triangle ABC$ 的边 $BC$ 的中点，$E$ 是 $BD$ 的中点。$O$ 是 $AE$ 的中点。要求：我们必须证明 $ar(\triangle BOE) = \frac{1}{8} ar(\triangle ABC)$。解答：连接 $BO, AE$ 和 $AD$。在 $\triangle ABC$ 中，$D$ 是 $BC$ 的中点$\operatorname{ar}(\triangle ABD)=\operatorname{ar}(\Delta ADC)=\frac{1}{2} \operatorname{ar}(\Delta ABC)$在 $\triangle ABD$ 中，$E$ 是 $BD$ 的中点。这意味着 $\operatorname{ar}(\Delta ABE)=\frac{1}{2} \operatorname{ar}(\Delta ABD)$$=\frac{1}{2}\left(\frac{1}{2} \operatorname{ar}(\Delta ABC)\right)$$=\frac{1}{4} \operatorname{ar}(\triangle ABC)$$O$ 是 $AE$ 的中点因此，$ar(\Delta BOE)=\frac{1}{2} ar(\Delta ABE)$$=\frac{1}{2} \times(\frac{1}{4} ar(\Delta ABC))$$=\frac{1}{8} ar(\Delta ABC)$$\operatorname{ar}(\Delta BOE)=\frac{1}{8} \operatorname{ar}(\Delta ABC)$证毕。阅读更多
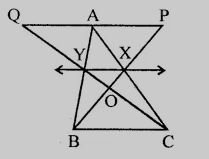
"\已知：$X$和$Y$分别是$AC$和$AB$的中点，$QP \parallel BC$，$CYQ$和$BXP$是直线。
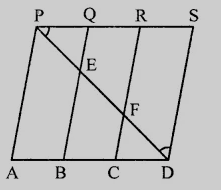
"\已知：$PSDA$是一个平行四边形，其中$PQ = QR = RS$，且$AP \parallel BQ \parallel CR$。