数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
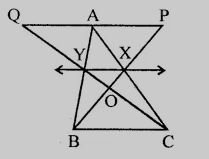
法学如图所示，X和Y分别是AC和AB的中点，QP∥BC，CYQ和BXP是直线。证明ar(△ABP) = ar(△ACQ)。
已知
X和Y分别是AC和AB的中点，QP∥BC，CYQ和BXP是直线。
要求
我们必须证明ar(△ABP) = ar(△ACQ)。
解答
X和Y分别是AC和AB的中点。
这意味着：
XY∥BC
同样地：
XY∥PQ
△BXY和△CXY同底XY，且在同一对平行线之间。
这意味着：
ar(△BXY) = ar(△CXY)……(i)
梯形XYAP和梯形XYAQ同底XY，且在同一对平行线之间。
这意味着：
ar(XYAP) = ar(XYAQ)……(ii)
(i)和(ii)相加，得到：
ar(△BXY) + ar(XYAP) = ar(△CXY) + ar(XYAQ)
ar(△ABP) = ar(△ACQ)。
证毕。
更新于：2022年10月10日
49 次浏览
广告