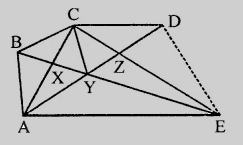
如图所示，$CD \parallel AE$ 且 $CY \parallel BA$。
证明：$ar(\triangle ZDE) = ar(\triangle CZA)$。
"\n

已知

$CD \parallel AE$ 且 $CY \parallel BA$。

题目

我们必须证明 $ar(\triangle ZDE) = ar(\triangle CZA)$。

解答

$\triangle ADE$ 和 $\triangle ACE$ 同底 $AE$，且在同一直线之间。

因此，

$ar(\triangle ADE) = ar(\triangle ACE)$

从两边减去 $ar(\triangle AZE)$，得到：

$ar(\triangle ADE) - ar(\triangle AZE) = ar(\triangle ACE) - ar(\triangle AZE)$

$ar(\triangle ZDE) = ar(\triangle ACZ)$

$ar(\triangle ZDE) = ar(\triangle CZA)$

证毕。

教程点

更新于：2022年10月10日

49 次浏览

开启您的职业生涯

完成课程获得认证

开始学习