已知:$ABC$ 是一个直角三角形,∠A 为直角,$BCED$、$ACFG$ 和 $ABMN$ 分别是边 $BC$、$CA$ 和 $AB$ 上的正方形。线段 $AX \perp DE$ 交 $BC$ 于 $Y$。要求:我们必须证明 $\triangle MBC \cong \triangle ABD$。解答:在 $\triangle MBC$ 和 $\triangle ABD$ 中,$MB=AB$ (正方形的边)$BC = BD$$\angle MBC = \angle ABD = 90^o + \angle ABC)$因此,根据 SAS 公理,$\triangle MBC \cong \triangle ABD$这意味着,$ar(\triangle MBC) = ar(\triangle ABD)$........…(i)证毕。
已知:在 $\triangle ABC$ 中,$L$ 和 $M$ 分别是 $AB$ 和 $AC$ 上的点,使得 $LM \| BC$。要求:我们必须证明 $ar(\triangle LBC) = ar(\triangle MBC)$。解答:连接 $LM$、$LC$ 和 $MB$。$L$ 和 $M$ 是 $AB$ 和 $AC$ 的中点。这意味着,$LM \| BC$$\triangle LBM$ 和 $\triangle LCM$ 具有相同的底 $LM$ 且位于相同的平行线之间。因此,$ar(\triangle LBM) = ar(\triangle LCM)$......…(i)$ar(\triangle LCM) = ar(\triangle LBM)$\triangle LBC$ 和 $\triangle MBC$ 具有相同的底 $BC$ 且位于相同的平行线之间。因此,$ar(\triangle LBC) = ar(\triangle MBC)$......…(ii)证毕。 阅读更多
已知:在 $\triangle ABC$ 中,$L$ 和 $M$ 分别是 $AB$ 和 $AC$ 上的点,使得 $LM \| BC$。要求:我们必须证明 $ar(\triangle ABM) = ar(\triangle ACL)$。解答:连接 $LM$、$LC$ 和 $MB$。$L$ 和 $M$ 是 $AB$ 和 $AC$ 的中点。这意味着,$LM \| BC$$\triangle LBM$ 和 $\triangle LCM$ 具有相同的底 $LM$ 且位于相同的平行线之间。因此,$ar(\triangle LBM) = ar(\triangle LCM)$......…(i)$ar(\triangle LCM) = ar(\triangle LBM)$\triangle LBC$ 和 $\triangle MBC$ 具有相同的底 $BC$ 且位于相同的平行线之间。因此,$ar(\triangle LBC) = ar(\triangle MBC)$......…(ii)$ar(\triangle LMB) = ar(\triangle LMC)$ ... 阅读更多
已知:在 $\triangle ABC$ 中,$L$ 和 $M$ 分别是 $AB$ 和 $AC$ 上的点,使得 $LM \| BC$。要求:我们必须证明 $ar(\triangle LOB) = ar(\triangle MOC)$。解答:连接 $LM$、$LC$ 和 $MB$。$L$ 和 $M$ 是 $AB$ 和 $AC$ 的中点。这意味着,$LM \| BC$$\triangle LBM$ 和 $\triangle LCM$ 具有相同的底 $LM$ 且位于相同的平行线之间。因此,$ar(\triangle LBM) = ar(\triangle LCM)$......…(i)$ar(\triangle LCM) = ar(\triangle LBM)$\triangle LBC$ 和 $\triangle MBC$ 具有相同的底 $BC$ 且位于相同的平行线之间。因此,$ar(\triangle LBC) = ar(\triangle MBC)$......…(ii)$ar(\triangle LMB) = ar(\triangle LMC)$ ... 阅读更多
已知:$ABC$ 和 $BDC$ 是两个等边三角形,其中 $D$ 是 $BC$ 的中点。$AE$ 交 $BC$ 于 $F$。要求:我们必须证明 \( \operatorname{ar}(\triangle \mathrm{BDE})=\frac{1}{4} \operatorname{ar}(\Delta \mathrm{ABC}) \)。解答:设 $\mathrm{AB}=\mathrm{BC}=\mathrm{CA}=x$这意味着,$\mathrm{BD}=\frac{x}{2}$ ($\mathrm{D}$ 是 $\mathrm{BC}$ 的中点)等边三角形 $\mathrm{ABC}$ 的面积 $=\frac{\sqrt{3}}{4}(\text { side })^{2}$$=\frac{\sqrt{3}}{4} x^{2} \mathrm{~cm}^{2}$等边三角形 $\mathrm{BED}$ 的面积 $=\frac{\sqrt{3}}{4}(\frac{x}{2})^{2}$$=\frac{\sqrt{3}}{4} \times \frac{x^{2}}{4}$$=\frac{1}{4}(\frac{\sqrt{3}}{4} x^{2})$$=\frac{1}{4}(\text { area of } \triangle \mathrm{ABC})$证毕。阅读更多
已知:在 $\triangle ABC$ 中,$L$ 和 $M$ 分别是 $AB$ 和 $AC$ 上的点,使得 $LM \| BC$。要求:我们必须证明 $ar(\triangle LCM) = ar(\triangle LBM)$。解答:连接 $LM$、$LC$ 和 $MB$。$L$ 和 $M$ 是 $AB$ 和 $AC$ 的中点。这意味着,$LM \| BC$$\triangle LBM$ 和 $\triangle LCM$ 具有相同的底 $LM$ 且位于相同的平行线之间。因此,$ar(\triangle LBM) = ar(\triangle LCM)$......…(i)$ar(\triangle LCM) = ar(\triangle LBM)$证毕。
已知:$ABCD$ 和 $AEFD$ 是两个平行四边形。要求:我们必须证明 $ar(\triangle APE) : ar(\triangle PFA) = ar(\triangle QFD) : ar(\triangle PFD)$。解答:在 $\triangle AEP$ 和 $\triangle DFQ$ 中,$AE = DF$ (平行四边形的对边)$\angle AEP = \angle DFQ$ (对应角)$\angle APE = \angle DQF$ (对应角)因此,根据 AAS 公理,$\triangle AEP \cong \triangle DFQ$这意味着,$PE = QF$ (全等三角形对应边相等)$ar(\triangle AEP) = ar(\triangle DFQ)$.........(i)$\triangle PFA$ 和 $\triangle PFD$ 具有相同的底 $PF$ 且位于相同的平行线之间这意味着,$ar(\triangle PFA) = ar(\triangle PFD)$......…(ii)从 ... 阅读更多
已知:$ABCD$ 和 $AEFD$ 是两个平行四边形。要求:我们必须证明 $ar(\triangle PEA) = ar(\triangle QFD)$。解答:在 $\triangle AEP$ 和 $\triangle DFQ$ 中,$AE = DF$ (平行四边形的对边)$\angle AEP = \angle DFQ$ (对应角)$\angle APE = \angle DQF$ (对应角)因此,根据 AAS 公理,$\triangle AEP \cong \triangle DFQ$这意味着,$PE = QF$ (全等三角形对应边相等)$ar(\triangle PEA) = ar(\triangle QFD)$ 证毕。
正确答案:C. 灰尘 解释:灰尘减少了植物的光合作用,导致植物能量产生减少,从而导致植物受损。
正确答案:D. 紫外线 解释:臭氧层保护我们免受太阳的有害紫外线的伤害。

 数据结构
数据结构 网络
网络 RDBMS
RDBMS 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP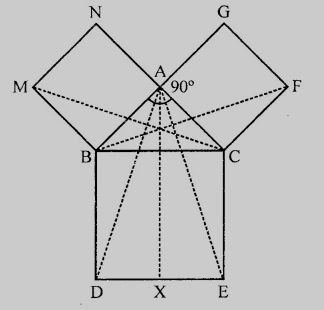 "\
"\
 "\
"\ "\
"\