数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法学
题目：我们需要化简以下表达式。解答：我们知道，$(a+b)^2=a^2+2ab+b^2$$(a-b)^2=a^2-2ab+b^2$因此，\( \begin{array}{l}( a) \ \left(\frac{1}{2} a-b\right)\left(\frac{1}{2} a+b\right)\left(\frac{1}{4} a^{2} +b^{2}\right) =\left(\frac{1}{4} a^{2} -b^{2}\right)\left(\frac{1}{4} a^{2} +b^{2}\right)\\=\left(\frac{1}{16} a^{4} -b^{4}\right)\\( b) \ \left(\frac{p}{2} -\frac{q}{3}\right)\left(\frac{p}{2} +\frac{q}{3}\right)\left(\frac{p^{2}}{4} +\frac{q^{2}}{9}\right)\left(\frac{p^{4}}{16} +\frac{q^{4}}{81}\right) =\left(\frac{p^{2}}{4} -\frac{q^{2}}{9}\right)\left(\frac{p^{2}}{4} +\frac{q^{2}}{9}\right)\left(\frac{p^{4}}{16} +\frac{q^{4}}{81}\right)\\=\left(\frac{p^{4}}{16} -\frac{q^{4}}{81}\right)\left(\frac{p^{4}}{16} +\frac{q^{4}}{81}\right)\\=\left(\frac{p^{8}}{256} -\frac{q^{8}}{6561}\right)\\( c) \ \left( a^{2} +1-a\right)\left( a^{2} -1+a\right) =\left[ a^{2} +( 1-a)\right]\left[ a^{2} -( 1-a)\right]\\=a^{4} -( 1-a)^{2}\\=a^{4} -\left( 1-2a+a^{2}\right)\\=a^{4} -1+2a-a^{2}\\=a^{4} -a^{2} +2a-1\\( d) \ \left( 4b^{2} +2b+1\right)\left( 4b^{2} -2b-1\right) =\left[ 4b^{2} +( 2b+1)\right]\left[ 4b^{2} -( 2b+1)\right]\\=\left( 4b^{2}\right)^{2} -( 2b+1)^{2}\\=16b^{4} -\left[( 2b)^{2} +2\times 2b\times 1+1^{2}\right]\\=16b^{4} -4b^{2} -4b-1\end{array}\)阅读更多
已知：已知表达式为 $x+\frac{1}{x}=11$。题目：我们需要求解a) $x^{2}+\frac{1}{x^{2}}$ b) $x^{4}+\frac{1}{x 4}$的值。解答：a) $x^{2}+\frac{1}{x^{2}}$ $x+\frac{1}{x}=11$两边平方， $(x+\frac{1}{x})^2=(11)^2$$x^2 + \frac{1}{x^2} +2.x.\frac{1}{x} = 121$ $[(a+b)^2=a^2+b^2+2ab]$$x^2 + \frac{1}{x^2} +2=121$$x^2 + \frac{1}{x^2} =121-2$$x^2 + \frac{1}{x^2} =119$.因此，$x^2 + \frac{1}{x^2}$的值为 119。 b) $x^{4}+\frac{1}{x 4}$我们知道， $x^2 + \frac{1}{x^2} =119$两边平方， $(x^2 + \frac{1}{x^2})^2 =(119)^2$$(x^2)^2 + (\frac{1}{x^2})^2 +2 .x^2.\frac{1}{x^2}=14161$ $[(a+b)^2=a^2+b^2+2ab]$$x^4 + \frac{1}{x^4} + 2 = 14161$$x^4 + \frac{1}{x^4}=14161-2$$x^4 + \frac{1}{x^4}=14159$.因此，$x^4 + \frac{1}{x^4}$的值为 14159。阅读更多
已知：已知表达式为 $x-\frac{1}{x}=5$。题目：我们需要求解a) $x^{2}+\frac{1}{x^{2}}$b) $x^{4}+\frac{1}{x 4}$的值。解答：a) $x^{2}+\frac{1}{x^{2}}$ $x-\frac{1}{x}=5$两边平方， $(x-\frac{1}{x})^2=(5)^2$$x^2 + \frac{1}{x^2} -2.x.\frac{1}{x} = 25$ $[(a-b)^2=a^2+b^2-2ab]$$x^2 + \frac{1}{x^2} -2=25$$x^2 + \frac{1}{x^2} =25+2$$x^2 + \frac{1}{x^2} =27$.因此，$x^2 + \frac{1}{x^2}$的值为 27。 b) $x^{4}+\frac{1}{x 4}$我们知道， $x^2 + \frac{1}{x^2} =27$两边平方， $(x^2 + \frac{1}{x^2})^2 =(27)^2$$(x^2)^2 + (\frac{1}{x^2})^2 +2 .x^2.\frac{1}{x^2}=27^2$ $[(a+b)^2=a^2+b^2+2ab]$$x^4 + \frac{1}{x^4} + 2 = 729$$x^4 + \frac{1}{x^4}=729-2$$x^4 + \frac{1}{x^4}=727$.因此，$x^4 + \frac{1}{x^4}$的值为 727。阅读更多
已知：已知表达式为 \( x^{2}+\frac{1}{x^{2}}=62 \)。题目：我们需要求解(a) \( x+\frac{1}{x} \)(b) \( x-\frac{1}{x} \)的值。解答：a) $x^{2}+\frac{1}{x^{2}}=62$两边加2，得到，$x^2+\frac{1}{x^2}+2=62+2$$(x)^2+(\frac{1}{x})^2+2.x.\frac{1}{x}=64$$(x+\frac{1}{x})^2=8^2$ $[(a+b)^2=a^2+b^2+2ab]$$\Rightarrow x+\frac{1}{x}=8$b) $x^{2}+\frac{1}{x^{2}}=62$两边减2，得到，$x^2+\frac{1}{x^2}-2=62-2$$(x)^2+(\frac{1}{x})^2-2.x.\frac{1}{x}=60$$(x-\frac{1}{x})^2=(\sqrt{60})^2$ $[(a-b)^2=a^2+b^2-2ab]$$\Rightarrow x-\frac{1}{x}=\sqrt{60}$
题目：我们需要改正以下表达式的错误。(a) \( (2 x+5)^{2}=4 x^{2}+25 \)(b) \( \left(x-\frac{1}{2}\right)\left(x-\frac{1}{2}\right)=x^{2}-\frac{1}{4} \)(c) \( (5 a-b)^{2}=10 a^{2}-5 a b+b^{2} \)(d) \( (p-3)(p-7)=p^{2}+21 \)解答：我们知道，$(a+b)^2=a^2+2ab+b^2$$(a-b)^2=a^2-2ab+b^2$因此， (a) 左侧 $=(2x+5)^2$$=(2x)^2+2.(2x).(5)+(5)^2$$=4x^2+20x+25$右侧 $=4x^2+25$因此，我们需要在右侧加上 $20x$(b) 左侧 $=(x-\frac{1}{2})(x-\frac{1}{2})$$=(x-\frac{1}{x})^2$$=x^2-2.x.\frac{1}{x}+(\frac{1}{x})^2$$=x^2-2+\frac{1}{x^2}$右侧 $=x^{2}-\frac{1}{4}$因此，我们需要将右侧的$-\frac{1}{4}$ 替换为 $-2+\frac{1}{x^2}$(c) 左侧 $=(5 a-b)^{2}$$=(5a)^2-2.5a.b+(b)^2$$=25a^2-10ab+b^2$右侧 $=10 a^{2}-5 a b+b^{2}$因此，我们需要将右侧的$10 a^{2}-5 a b$ 替换为 $25a^2-10ab$。(d) 左侧 $=(p-3)(p-7)$$=p(p)-p(7)-3(p)-3(-7)$$=p^2-7p-3p+21$$=p^2-10p+21$右侧 $=p^{2}+21$因此，我们需要在右侧加上 $-10p$。
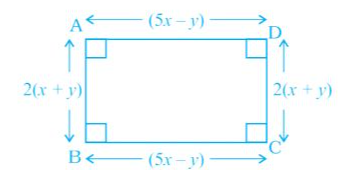
阅读更多
"\题目：我们需要求解给定矩形的周长，并求当 \( x=1, \mathrm{y}=2 \) 时的值。解答：我们知道，长为 $l$，宽为 $b$ 的矩形的周长为 $2(l+b)$。因此，给定矩形的周长 $=2[(5x-y)+2(x+y)]$$=2(5x-y+2x+2y)$$=2(7x+y)$$=2(7x)+2(y)$$=14x+2y$当 \( x=1, \mathrm{y}=2 \) 时，矩形的周长为，周长 $=14(1)+2(2)$$=14+4$$=18$。
正确答案：(c) 分液漏斗 解释：由于牛奶和花生油是两种互不相溶的液体，因此可以使用分液漏斗将它们分离。
正确答案：(c) 沙子和硫磺 解释：沙子和硫磺的混合物不能用水作为溶剂分离，因为两者都不溶于水。
正确答案：(d) 二硫化碳 解释：硫溶于二硫化碳，而炭不溶，因此它可以用来分离炭粉和硫粉的混合物。
正确答案：(d) 色谱法 解释：色谱法是一种用于分离混合物成分的技术，其中溶质颗粒的数量极少。因此，钢笔墨水中存在的染料可以通过色谱法分离。