数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：矩形的邻边分别为 $x- 3y+5z$ 和 $3x- 5y-2z$。求解：求矩形的周长。解：设 $l=x- 3y+5z$ 和 $b=3x- 5y-2z$矩形的周长 $=2(l+b)$因此，周长 $=2(x- 3y+5z+3x- 5y-2z)$$=2[(x+3x)+(-3y-5y)+(5z-2z)]$$=2(4x-8y+3z)$$=8x-16y+6z$矩形的周长为 $8x-16y+6z$。
对于前 100 公里：距离$=100\ 公里$速度$=50\ 公里/小时$因此，旅程第一部分所需时间 $t_2=\frac{距离}{速度}=\frac{100}{50}=2\ 小时$对于旅程的第二部分：设火车在旅程第二部分的速度为 $s\ 公里/小时$：距离$=100\ 公里$旅程第二部分所需时间 $t_2=\frac{距离}{速度}=\frac{100}{s}$现在，我们知道：$平均速度=\frac{总行程}{总时间}$其中，平均速度$=70\ 公里/小时$总行程$=200\ 公里$总时间 $t=t_1+t_2=2+\frac{100}{s}$将这些值代入平均速度方程，我们得到：平均速度$=\frac{总行程}{总时间}$或， $70=\frac{200}{( 2 + \frac{100}{s})}$或， $70\times( 2 + \frac{100}{s})=200$或， $140 + \frac{7000}{s}=200$或， $\frac{7000}{s}=60$或， $s=\frac{7000}{60}=116.67\ 公里/小时$因此，火车的速度必须为 $116.67\ ... 阅读更多
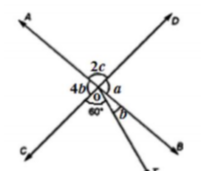
"\已知：两条直线 \( \mathrm{AB} \& \mathrm{CD} \) 相交于 \( \mathrm{O} \)。 \( \angle \mathrm{COT}=60^{\circ} \)，求解：求 \( \mathrm{a}, \mathrm{b}, \mathrm{c} \)。解：我们知道，对顶角相等。一条直线上的角的和为 $180^o$。一个点周围的角的和为 $360^o$。因此， $a=4b$....(i)$4b+60^o+b=180^o$$\Rightarrow 5b=180^o-60^o$$\Rightarrow 5b=120^o$$\Rightarrow b=\frac{120^o}{5}$$\Rightarrow b=24^o$$a=4(24^o)$$=96^o$$4b+2c=180^o$$4(24^o)+2c=180^o$$96^o+2c=180^o$$2c=180^o-96^o$$2c=84^o$$c=\frac{84^o}{2}$$c=42^o$因此， $\mathrm{a}=96^o, \mathrm{b}=24^o, \mathrm{c}=42^o$。阅读更多
求解：计算给定代数表达式之和。解：a) \( x+5 \) 和 \( x+3 \)$(x+5)+(x+3)=(x+x)+(5+3)$$=2x+8$b) \( 3 x+4 \) 和 \( 4 x+9 \)$(3x+4)+(4x+9)=(3x+4x)+(4+9)$$=7x+13$c) \( 5 y-2 \) 和 \( 2 y+7 \)$(5y-2)+(2y+7)=(5y+2y)+(-2+7)$$=7y+5$ d) \( 8 y-3 \) 和 \( 5 y-6 \)$(8y-3)+(5y-6)=(8y+5y)+(-3-6)$$=13y-9$
已知：$(-31)+17-(29)$求解：化简给定表达式。解：我们知道，$(+) \times (+) = (-) \times (-) = (+)$$(+) \times (-) = (-) \times (+) = (-)$ 因此，$(-31)+17-(29)=17+(-31-29)$$=17+(-60)$$=17-60$$=-43$$(-31)+17-(29)=-43$
已知：给定的有理数是 $\frac{2}{3}$。求解：将给定的有理数表示为小数。解：通过长除法，我们得到，3)2.00(0.66 18-------- 20 18-------- 2$\frac{2}{3}=0.\overline{6}$因此，$\frac{2}{3}$ 可以表示为 $ 0.\overline{6}$。
已知：给定的有理数是 $-\frac{4}{9}$。求解：将给定的有理数表示为小数。解：通过长除法，我们得到，9)4.00(0.44 36-------- 40 36-------- 4$\frac{4}{9}=0.\overline{4}$$\Rightarrow -\frac{4}{9}=-0.\overline{4}$因此，$-\frac{4}{9}$ 可以表示为$ -0.\overline{4}$。
已知：给定的有理数是 $-\frac{2}{15}$。求解：将给定的有理数表示为小数。解：通过长除法，我们得到，15)2.00(0.133 15-------- 50 45-------- 50 45----------- 5$\frac{2}{15}=0.1\overline{3}$$\Rightarrow -\frac{2}{15}=-0.1\overline{3}$因此，$-\frac{2}{15}$ 可以表示为$ -0.1\overline{3}$。
已知：给定的有理数是 $-\frac{22}{13}$。求解：将给定的有理数表示为小数。解：通过长除法，我们得到，13)22(1.6923076 13-------- 90 78-------- 120 117----------- 30 26------------ 40 39------------- 100 91--------------- 90 78----------------- 12$-\frac{22}{13}=1.\overline{692307}$$\Rightarrow -\frac{22}{13}=-1.\overline{692307}$因此，$-\frac{22}{13}$ 可以表示为$ -1.\overline{692307}$。