数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：给定的有理数是 $\frac{437}{999}$。要求：我们要将给定的有理数表示为小数。解：用长除法，得到，999)437.0(0.437 3996-------------- 3740 2997-------------- 7430 6993---------------- 437$\frac{437}{999}=0.\overline{437}$因此，$\frac{437}{999}$ 可以表示为 $ 0.\overline{437}$.
已知：给定的有理数是 $\frac{33}{26}$。要求：我们要将给定的有理数表示为小数。解：用长除法，得到，26)33(1.269230769 26-------- 70 52-------- 180 156----------- 240 234------------ 60 52------------- 80 78--------------- 200 182----------------- 180 156------------------ 240 236--------------------- 4$\frac{33}{26}=1.2\overline{692307}$因此，$\frac{33}{26}$ 可以表示为 $ 1.2\overline{692307}$.
要求：我们必须猜出在给定条件下 $q$ 必须满足的性质。解：一些具有有限小数表示的有理数是：$\frac{1}{2}=0.5$$\frac{1}{4}=0.25$$\frac{1}{5}=0.2$$\frac{1}{10}=0.1$我们可以观察到，如果我们有一个有理数 $\frac{p}{q}$，其中 $p$ 和 $q$ 是互质的，并且 $q$ 的质因数分解形式为 $2^n.5^m$，其中 $n$ 和 $m$ 是非负整数，则 $\frac{p}{q}$ 具有有限展开。该性质是如果分母有因子 2 或 5 或两者都有，则小数表示将是有限的。
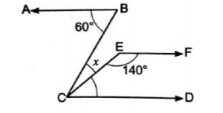
"\已知：$AB \parallel CD \parallel EF$。要求：我们必须找到 $x$ 的值。解：设 $\angle ECD=y$$CD \parallel EF$ 且 $CE$ 是横截线。这意味着，$\angle ECD$ 和 $\angle CEF$ 是同旁内角。$\angle ECD+\angle CEF=180^o$ $y+140^o=180^o$$y=180^o-140^o$$y=40^o$$AB \parallel CD$ 且 $BC$ 是横截线。这意味着，$\angle BCD$ 和 $\angle ABC$ 是内错角。$\angle ABC=\angle BCD$$60^o=x+y$$60^o=x+40^o$$x=60^o-40^o$$x=20^o$ $x$ 的值为 $20^o$。
已知：一个水桶形状是圆锥的台体，高为 $30\ cm$，上下底面半径分别为 $10\ cm$ 和 $20\ cm$。要求：我们必须找到水桶的容积和表面积以及能完全装满容器的牛奶的成本，牛奶价格为每升 25 元。解：水桶的高度 $h=30\ cm$水桶的上底面半径 $r_1=20\ cm$水桶的下底面半径 $r_2=10\ cm$因此，水桶的容积（体积）$=\frac{\pi}{3}[r_{1}^{2}+r_{2}^{2}+r_{1} r_{2}]h$$=\frac{3.14 \times 30}{3}[20^{2}+10^{2}+20 \times 10] \mathrm{cm}^{3}$$=21980\ cm^3$$=21.980$ 升母线长 $l=\sqrt{h^{2}+\left(r_{1}-r_{2}\right)^{2}}$$=\sqrt{900+100}$$=31.62 \mathrm{~cm}$水桶的表面积 ... 阅读更多
已知：圆锥体高为 \( 10 \mathrm{~cm} \)。用一个平行于底面的平面将圆锥体分成两部分，平面通过圆锥体高度的中点。要求：我们必须找到这两部分体积的比值。解：圆锥体底面半径 $r = 10\ cm$设圆锥体的总高度为 $h$。在 $\triangle AOB$ 中，$C$ 是 $AO$ 的中点，且 $CD\ \parallel\ OB$因此，$\frac{\mathrm{OB}}{\mathrm{CD}}=\frac{\mathrm{AO}}{\mathrm{AC}}$$\Rightarrow \frac{10}{\mathrm{CD}}=\frac{h}{\frac{h}{2}}$$\Rightarrow \frac{10}{\mathrm{CD}}=\frac{2}{1}$$\Rightarrow \mathrm{CD}=\frac{10}{2}=5 \mathrm{~cm}$这意味着， $r_{2}=5 \mathrm{~cm}$较小圆锥的体积 $=\frac{1}{3} \pi r_{2}^{2} \frac{h}{2}$$=\frac{1}{3} \pi \times 5^2 \times \frac{h}{2}$$=\frac{25}{6} \pi h$台体的体积 $=\frac{1}{3} ... 阅读更多
已知：一个用金属板制成的水桶形状是圆锥体，高为 \( 35 \mathrm{~cm} \)，上下底面半径分别为 \( 30 \mathrm{~cm} \) 和 \( 12 \mathrm{~cm} \)。牛奶售价为每升 \( ₹ 40 \)。要求：我们必须找到如果水桶装满，它能装多少升牛奶以及此人获得的金额。解：水桶（圆锥台体）的半径为 $= 30\ cm$ 和 $12\ cm$$r_1=30\ cm$$r_2=12\ cm$水桶的深度 $h= 35\ cm$因此，水桶的容积（体积）$=\frac{1}{3} ... 阅读更多
**已知：**一个桶形如圆台，底面和顶面的直径分别为\( 10 \mathrm{~cm} \)和\( 30 \mathrm{~cm} \)，高为\( 24 \mathrm{~cm} \)。**求：**制作该桶所需的金属板面积。**解：**由于底面和顶面的直径分别为 $10\ cm$ 和 $30\ cm$。因此，底面半径 $r=\frac{10}{2}$$=5\ cm$顶面半径 $R=\frac{30}{2}$$=15\ cm$圆台的高 $h=24\ cm$设圆台的母线长为 $l$。我们知道，$l^{2}=h^{2}+( R-r)^{2}$$\Rightarrow l^{2}=(24)^{2}+( 15-5)^{2}$$\Rightarrow l^{2}=576+100=676$$\Rightarrow ... 阅读更多
**已知：**一个水库呈圆台形，容积为\( 44 \times 10^{7} \)升，水库完全注满水。水库底部和顶部的半径分别为 50 米和 100 米。**求：**水深和水库的侧面积。**解：**水库顶部的半径 $r_1 = 100\ m$水库底部的半径 $r_2 = 50\ m$水库的容量 $= 44 \times 10^7$ 升因此，体积 $=\frac{44 \times 10^{7}}{1000} \mathrm{~m}^{3}$$=\frac{44 \times 10^{7}}{10^{3}}$$=44 \times 10^{7-3}$$=44 \times 10^{4} \mathrm{~m}^{3}$$=440000 \mathrm{~m}^{3}$设水深为 $h$。 ... 阅读更多
**已知：**给定项为 $(x + 1)$。给定的多项式为(i) \( x^{3}+x^{2}+x+1 \) (ii) \( x^{4}+x^{3}+x^{2}+x+1 \)(iii) \( x^{4}+3 x^{3}+3 x^{2}+x+1 \)(iv) \( x^{3}-x^{2}-(2+\sqrt{2}) x+\sqrt{2} \) **求：**我们必须检查给定的多项式是否以 $(x + 1)$ 为因式。**解：**根据因式定理，如果 $(x+1)$ 是给定多项式 $P(x)$ 的因式，那么当 $x= -1$ 时，$p(x)=0$。(i) $x^{3}+x^{2}+x+1$ 设 $p(x)= x^{3}+x^{2}+x+1$将 $x= -1$ 代入 $p(−1)=(−1)^3+(−1)^2+(−1)+1 =−1+1−1+1=0$因此，根据因式定理，$x+1$ 是 $x^{3}+x^{2}+x+1$ 的因式。(ii) $x^{4}+x^{3}+x^{2}+x+1 $ 设 $p(x)=x^{4}+x^{3}+x^{2}+x+1 $将 $x= -1$ 代入 $p(−1)=(−1)^4+(-1)^3+(−1)^2+(−1)+1 =1−1+1−1+1=1$因此，根据因式定理，$x+1$ 不是 $x^{4}+x^{3}+x^{2}+x+1$ 的因式。(iii) $x^{4}+3x^{3}+3x^{2}+x+1 $ 设 $p(x)=x^{4}+3x^{3}+3x^{2}+x+1 $将 $x= -1$ 代入 $p(−1)=(−1)^4+3(-1)^3+3(−1)^2+(−1)+1 =1−3+3−1+1=1$因此，根据因式定理， ... 阅读更多