数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律研究
已知：四个半径为$a$的等圆彼此相切。求解：我们必须证明它们之间的面积为\( \frac{6}{7} a^{2} \)。解：每个圆的半径$= a$。四个圆彼此外切，这意味着通过连接圆心可以得到一个正方形。正方形每边的长度$=a + a = 2a$正方形的面积$= (2a)^2$$= 4a^2$正方形内四个象限的面积$= 4 \times \frac{1}{4} \pi a^2$$= \pi a^2$$= \frac{22}{7} \times a^2$因此，圆之间部分的面积$=$正方形的面积$-$四个象限的面积… 阅读更多
"\已知：\(ABCDEF\)是一个以\(O\)为中心的正六边形。三角形\(OAB\)的面积为9\(cm^2\)。求解：我们必须找到内接该正六边形的圆的面积。解：连接六边形的顶点与$O$，可以得到六个相等的等边三角形。等边三角形$OAB$的面积$= 9\ cm^2$。这意味着，六边形的面积$= 9 \times 6\ cm^2$$= 54\ cm^2$设圆的半径$= OB =AB = r$因此，$\frac{\sqrt{3}}{4} r^{2}=9$$\Rightarrow r^{2}=\frac{9 \times 4}{\sqrt{3}}$$\Rightarrow r^{2}=\frac{36}{\sqrt{3}}$圆的面积$=\pi r^{2}$$=\frac{22}{7} \times ... 阅读更多
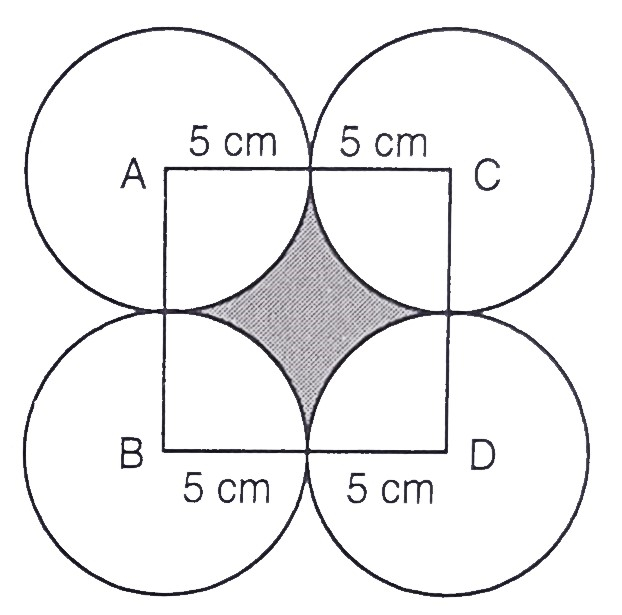
"\已知：四个等圆，每个半径为\(5cm\)，如图所示彼此相切。求解：我们必须求它们之间的面积。解：每个圆的半径$= 5\ cm$。四个圆彼此外切，这意味着通过连接圆心可以得到一个正方形。正方形每边的长度$=5 + 5 = 10\ cm$正方形的面积$= (10)^2$$= 100\ cm^2$正方形内四个象限的面积$= 4 \times \frac{1}{4} \pi r^2$$= \pi r^2$$= 3.14 \times 5^2\ cm^2$$= 3.14 \times 25\ cm^2$$= 78.5\ cm^2$因此，部分的面积… 阅读更多
"\已知：\(ABCDEF\)是一个以\(O\)为中心的正六边形。三角形\(OAB\)的面积为9\(cm^2\)。求解：我们必须找到六边形的面积。解：连接六边形的顶点与$O$，可以得到六个相等的等边三角形。等边三角形$OAB$的面积$= 9\ cm^2$。这意味着，六边形的面积$= 9 \times 6\ cm^2$$= 54\ cm^2$六边形的面积是$54 cm^2$。
已知：铅笔长$18cm$，直径$8mm$。求解：求铅笔直径与长度的比值。解：已知，铅笔长度$=18cm=180mm$铅笔直径$=8mm$因此，铅笔直径与长度的比值$=\frac{8}{180}$$=\frac{2}{45}$$=2:45$
化合物 元素(i) H2O (ii) CO (i) He (ii) Co (iii) Cl2
元素 化合物铁、硫、钠和碳 硫化铁、粉笔、苏打和尿素
糖的化学式为C12H22O11。因此，糖中存在的元素是碳(C)、氢(H)和氧(O)。氯化钠的化学式为NaCl。因此，氯化钠中存在的元素是钠(Na)和氯(Cl)。
纯净物是由相同类型的粒子或原子组成的。所有元素和化合物都是纯净物，因为它们包含相同类型的粒子。例如：氢气、二氧化碳。