已知:以等边三角形 ABC 的顶点 A 为圆心,画一个半径为 7 厘米的圆弧。求:阴影部分的面积。解:圆弧半径 r = 7 厘米等边三角形 ABC 边长 a = 14 厘米阴影区域面积 = 圆面积 + 等边三角形面积 - 2(未阴影扇形面积)=πr² + (√3/4)a² - 2 × πr² × θ/360° = 22/7 × 7² + 1.73/4 × 14² - 2 × 22/7 × 7² × 60°/360° ... 阅读更多
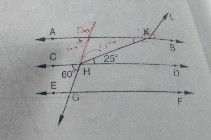
解:延长线段 GH 到 N,使其与线段 AB 相交于 M。AB||CD,GM 为横截线 ⇒ ∠AMH = ∠CHG = 60°(同位角)∠NMB = ∠AMH = 60°(对顶角)AB||CD,HK 为横截线 ⇒ ∠AKH = ∠KHD = 25°(内错角)NM||KL,KM 为横截线 ⇒ ∠NMK = ∠LKB = 60°(同位角)⇒ ∠LKM = 180° - ∠KLB(线性对)⇒ ∠LKM = 180° - 60° = 120° ⇒ ∠HKL = ∠HKA + ∠AKL ⇒ ∠HKL = 25° + 120° = 145° 阅读更多
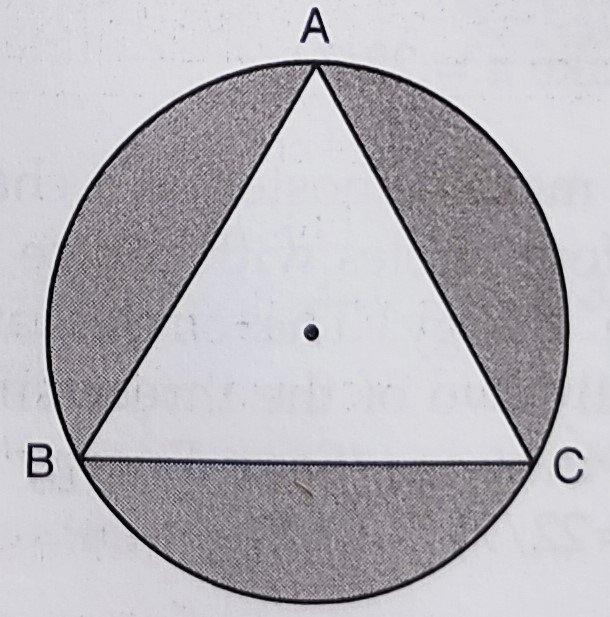
已知:一个边长为 6 厘米的等边三角形 ABC 内接于一个圆。求:阴影部分的面积。解:等边三角形 ABC 边长 = 6 厘米等边三角形面积 = (√3/4) × 6² = (√3/4) × 36 = 9√3 平方厘米 = 9 × 1.732 = 15.588 平方厘米作 AD⊥BC,AD 过圆心 O。这意味着,OA = (2/3)AD = (2/3) × (√3/2) × 6 = 2√3 厘米圆半径 r = 2√3 厘米因此,圆面积 = πr² = 22/7 × (2√3)² = 22/7 × … 阅读更多
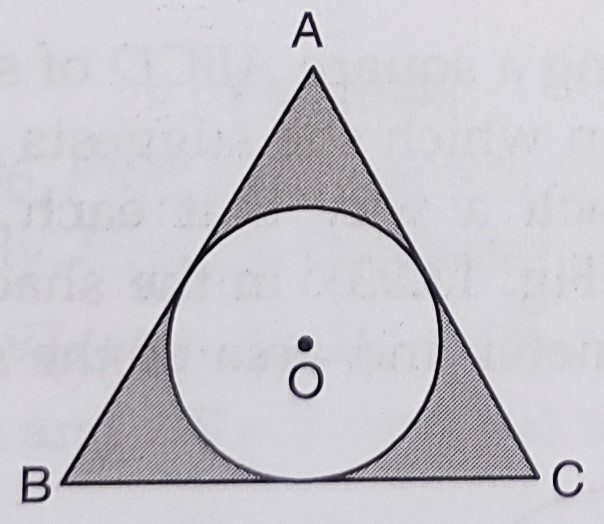
已知:一个圆内接于边长为 12 厘米的等边三角形 ABC,与三角形的边相切。求:内切圆的半径和阴影部分的面积。解:等边三角形 ABC 每条边的长度 a = 12 厘米这意味着,等边三角形的面积 = (√3/4)a² = (√3/4)(12)² = 1.732 × 12 × 12 / 4 = 62.352 平方厘米作 AD⊥BC。这意味着,OD = (1/3)(AD) (因为 O 是等边三角形的重心) = (1/3) × (√3/2) × 12 = √3/6 × 12 = 2√3内切圆半径 r = OD = 2√3 厘米内切圆面积 = … 阅读更多
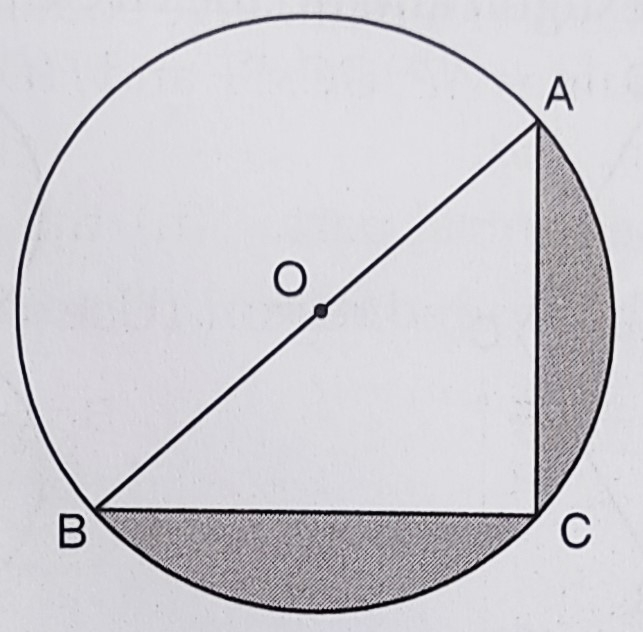
已知:AC=24 厘米,BC=10 厘米,O 是圆心。求:阴影部分的面积。解:在直角三角形 ABC 中,根据勾股定理,AB² = AC² + BC² = 24² + 10² = 576 + 100 = 676 = 26² ⇒ AB = 26 厘米圆的直径 = 26 厘米圆的半径 = 26/2 = 13 厘米阴影区域面积 = 半圆面积 - 直角三角形 ABC 面积 = (1/2)πr² - (1/2)AC × BC = (1/2)(3.14) × 13² - (1/2) × 24 × 10 = 265.33 - 120 = 145.33 平方厘米阴影区域的面积是 145.33 平方厘米。
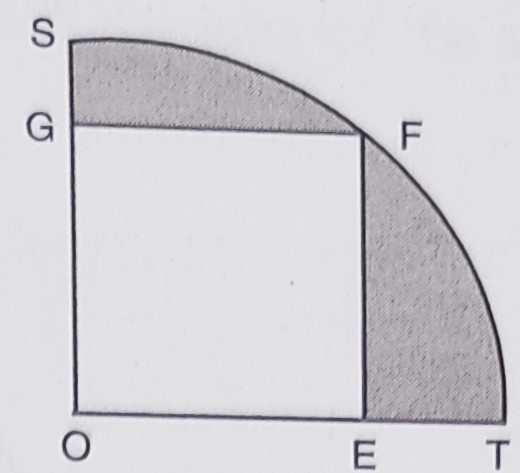
已知:OE=20 厘米。在扇形 OSFT 中内接正方形 OEFG。求:阴影部分的面积。解:正方形边长 s = 20 厘米这意味着,正方形对角线 = √2 × s = √2 × 20 = 20√2 厘米扇形半径 r = 20√2 厘米因此,四分之一圆面积 OTFS = (1/4) × πr² = (1/4)(3.14) × (20√2)² = (1/4) × 3.14 × 800 = 628 平方厘米正方形 OEFG 面积 = s² = 20² = 400 平方厘米阴影区域面积 = 四分之一圆面积 - 正方形面积 = 628 - 400 = 228 平方厘米阴影区域的面积是 228 平方厘米。阅读更多
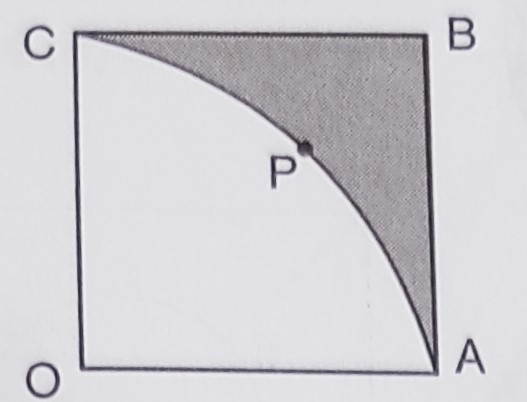
已知:\( O A B C \) 是边长为 \( 7 \mathrm{~cm} \) 的正方形。\( O A P C \) 是以 O 为圆心的一圆的四分之一圆。求:阴影部分的面积。解:正方形边长 $=7\ cm$正方形面积 $= (7)^2$$= 49\ cm^2$四分之一圆的半径 $= 7\ cm$因此,四分之一圆的面积 $=\frac{1}{4} \pi r^{2}$$=\frac{1}{4} \times \frac{22}{7} \times 7^2$$=\frac{77}{2}$$=38.5 \mathrm{~cm}^{2}$阴影部分面积 $=$ 正方形面积 $-$ 四分之一圆的面积$=49-38.5$$=10.5 \mathrm{~cm}^{2}$阴影部分的面积是 $10.5\ cm^2$。
已知:正方形 \( O A B C \) 内接于圆的四分之一圆 \( O P B Q \)。\( O A=21 \mathrm{~cm} \)。求:阴影部分的面积。解:由图可知,$OABC$ 是正方形。$OA = 21\ cm$连接 $OB$,则正方形的对角线 $\mathrm{OB}=\sqrt{2} \times \mathrm{OA}$$=\sqrt{2} \times 21 \mathrm{~cm}$$=21 \sqrt{2} \mathrm{~cm}$四分之一圆的半径 $=21 \sqrt{2} \mathrm{~cm}$因此,阴影部分面积 $=$ 四分之一圆面积 $-$ 正方形面积$=\frac{1}{4} \pi r^{2}-(\mathrm{OA})^{2}$$=\frac{1}{4} \times \frac{22}{7} \times(21 \sqrt{2})^{2}-(21)^{2}$$=\frac{11}{14} \times 441 \times 2-441$$=441(\frac{22}{14}-1)$$=441 \times \frac{8}{14}$$=252 \mathrm{~cm}^{2}$阴影部分的面积是 $252\ ... 阅读更多
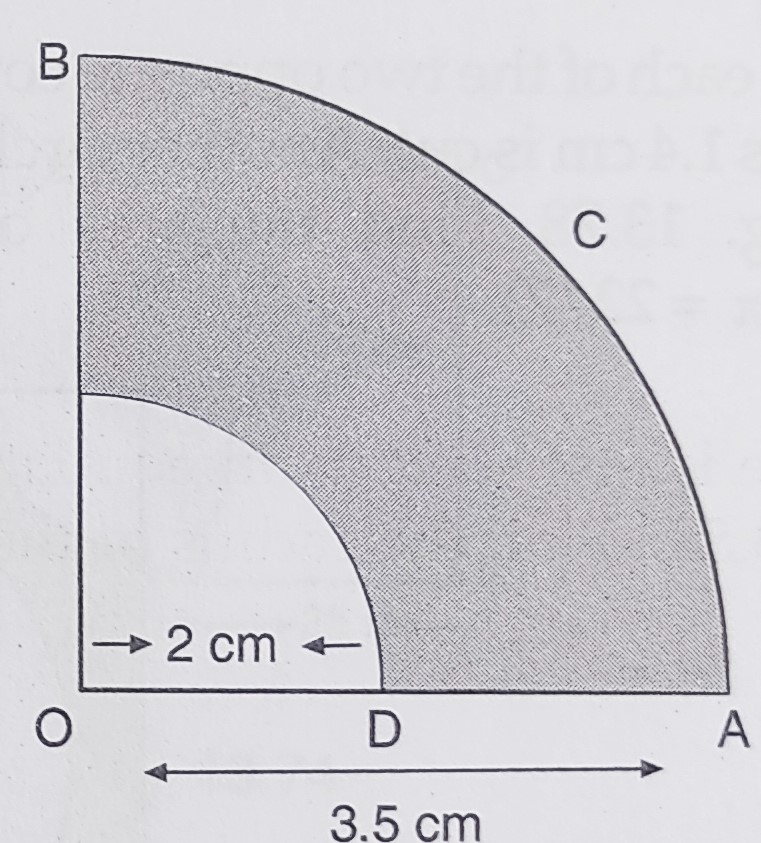
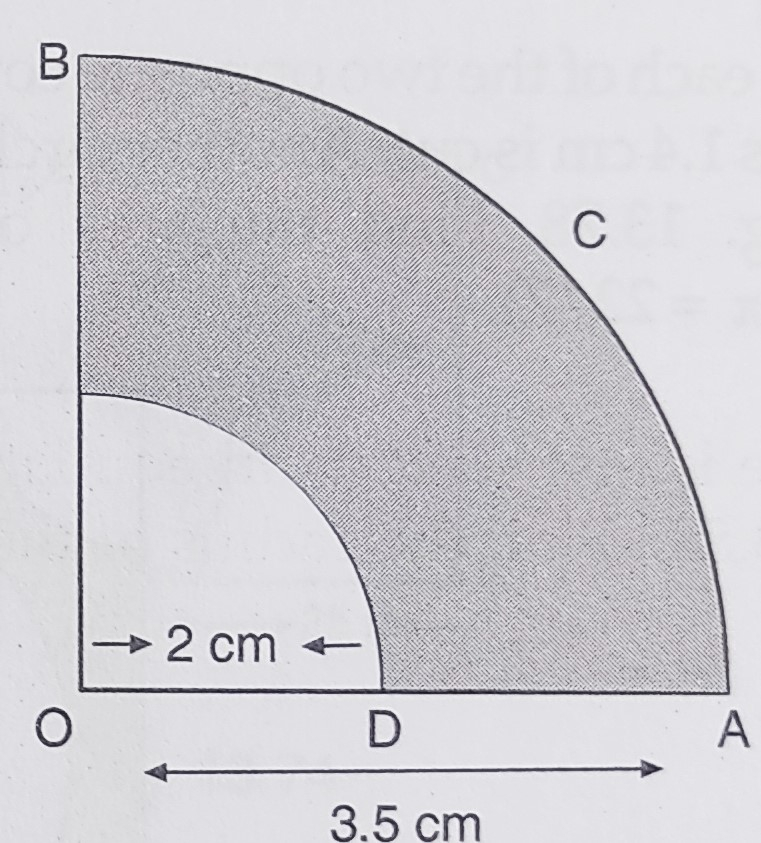
已知:\( O A C B \)是以 \( O \) 为圆心,半径为 \( 3.5 \mathrm{~cm} \) 的四分之一圆。\( O D=2 \mathrm{~cm} \)。求:阴影部分的面积。解:外侧四分之一圆的半径 $R = 3.5\ cm$内侧四分之一圆的半径 $r= 2\ cm$因此,阴影部分面积 $=$ 外侧四分之一圆面积 $-$ 内侧四分之一圆面积$=\frac{1}{4} \pi \mathrm{R}^{2}-\frac{1}{4} \pi r^{2}$$=\frac{1}{4}(\mathrm{R}^{2}-r^{2})$$=\frac{1}{4} \times \frac{22}{7}[(3.5)^{2}-(2)^{2}]$$=\frac{11}{14}(3.5+2)(3.5-2)$$=\frac{11}{14} \times 5.5 \times 1.5$$=6.482 \mathrm{~cm}^{2}$阴影部分的面积是 $6.482\ cm^2$。
已知:\( O A C B \)是以 \( O \) 为圆心,半径为 \( 3.5 \mathrm{~cm} \) 的四分之一圆。\( O D=2 \mathrm{~cm} \)。求:四分之一圆 \( O A C B \) 的面积。解:外侧四分之一圆的半径 $R = 3.5\ cm$内侧四分之一圆的半径 $r= 2\ cm$因此,四分之一圆 $OACB$ 的面积$=\frac{1}{4} \pi \mathrm{R}^{2}$$=\frac{1}{4} \times \frac{22}{7}(3.5)^{2}$$=\frac{1}{4} \times \frac{22}{7} \times 3.5 \times 3.5$$=9.625 \mathrm{~cm}^{2}$四分之一圆 \( O A C B \) 的面积是 $9.625\ cm^2$。

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP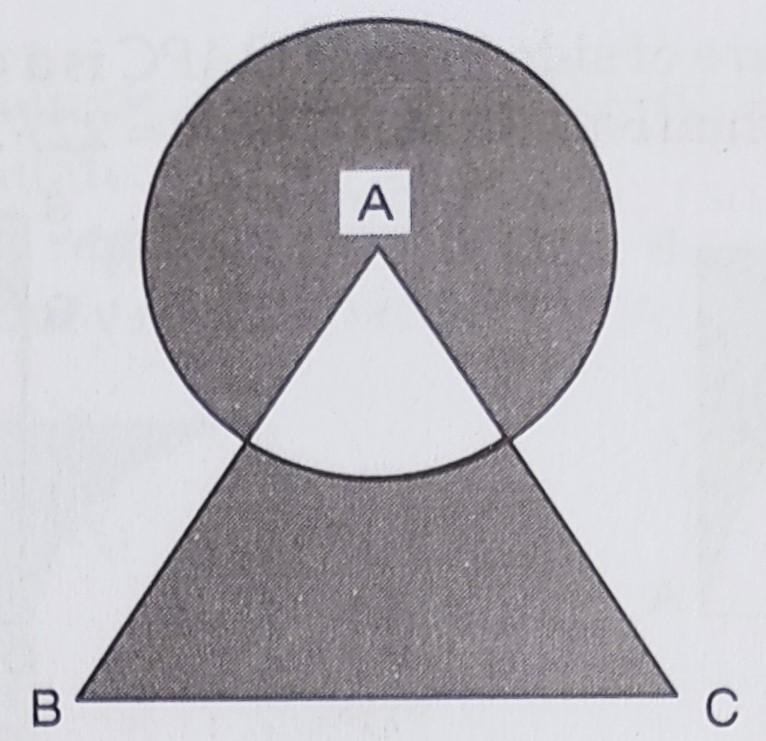 "\
"\
 "\
"\ "\
"\ "\p>
"\p>
 "\p>
"\p>
 "\p>
"\p>
 "\p>
"\p>
 "\
"\ "\
"\ "\
"\