数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
导致恒星闪烁的现象是光的折射。解释：当来自恒星的光进入地球大气层时，由于不同高度空气的光学密度不同，它会发生折射（弯曲）。大气层不断变化，导致来自恒星的光在不同时刻发生不同程度的折射。当大气层将更多星光折射到我们这里时，恒星看起来更亮；而当折射的星光较少时，它看起来则较暗。这样，由于……阅读更多
大气折射产生的两种效应是：(a) 恒星的闪烁。解释：当来自恒星的光进入地球大气层时，由于不同高度空气的光学密度不同，它会发生折射（弯曲）。大气层不断变化，导致来自恒星的光在不同时刻发生不同程度的折射。当大气层将更多星光折射到我们这里时，恒星看起来更亮；而当折射的星光较少时，它看起来则较暗。这样，到达我们眼睛的星光持续增加和减少……阅读更多
"\已知：ABCD 是一个矩形，其中 AB=14 cm，BC=7 cm。求解：我们必须找到阴影区域的面积。解：在 AD 和 BC 上分别以 AD 和 BC 为直径绘制两个半圆，在 CD 上绘制第三个半圆。矩形 ABCD 的面积 = 14 × 7 = 98 cm²在 AD 和 BC 上的两个半圆的半径 = AD/2 = 7/2 cm在 AD 和 BC 上的两个半圆的面积 = 2 × (1/2)πr² = (22/7) × (7/2) × (7/2) cm² = 77/2 cm²以 CD 为直径的半圆的半径 = CD/2 = 14/2 = 7 cm以 CD 为直径的半圆的面积……阅读更多
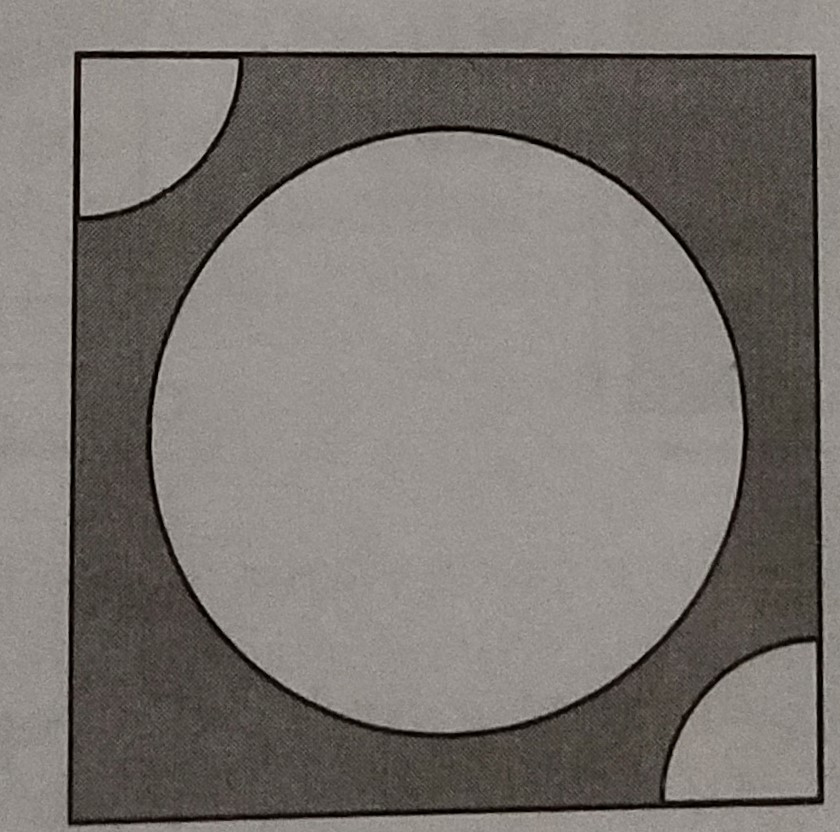
"\已知：从边长为 8 cm 的正方形的两个相对角中各切出一个半径为 1.4 cm 的圆的四分之一。还从中心切出一个半径为 4.2 cm 的圆，如图所示。求解：我们必须找到正方形剩余（阴影）部分的面积。解：正方形 ABCD 的边长 = 8 cm因此，正方形的面积 = (8)² = 64 cm²每个四分之一的半径 = 1.4 cm因此，两个四分之一的面积 = 2 × (1/4)πr² = (1/2) × (22/7)(1.4)² cm² = (1/2) × (22/7) × …阅读更多
"\已知：从矩形区域 ABCD（AB=20 cm）中切出一个直角三角形 AED（AE=9 cm，DE=12 cm）。在另一端，以 BC 为直径，在区域外部添加一个半圆。求解：我们必须找到阴影区域的面积。解：从图中，AB = 20 cm，AE = 9 cm，DE = 12 cm，∠AED = 90°在直角三角形 AED 中，根据勾股定理，AD² = AE² + DE² ⇒ AD = √(9² + 12²) = √(81 + 144) = √225 = 15 cm因此，三角形 AED 的面积……阅读更多
"\求解：我们必须找到给定图形的面积（单位：平方厘米），精确到小数点后一位。解：连接 AD。ABCD 是一个正方形。正方形每条边的长度 = 10 cm正方形的面积 = (10)² = 100 cm²半圆的半径 = 10/2 = 5 cm半圆的面积 = (1/2)πr² = (1/2) × (22/7) × 5 × 5 = 275/7 = 39.28 cm²因此，图形的总面积 = 100 - 24 + 39.28 = 76 + 39.28 = 115.28 cm² = 115.3 cm²给定图形的面积为 115.3 cm²。
我们眼睛的视网膜包含大量对光敏感的细胞。这些特化的细胞被称为感光细胞（对光敏感的细胞）。视网膜内存在两种不同类型的感光细胞：1. 视杆细胞 - 它们是杆状细胞，对光线和黑暗变化最敏感，因此在低光照条件下（暮光视觉）功能更好，在强光下会很快漂白。它们不适合颜色视觉。 人类视网膜中大约有 1.2 亿个视杆细胞。2. 视锥细胞 - 它们是锥形细胞，它们不像视杆细胞那样对光敏感。因此，它们在…… 阅读更多
已知：五年级男生人数是六年级男生人数的$\frac{9}{2}$倍。六年级有12名男生。求解：求五年级男生人数。解：六年级男生人数 = 12如题，五年级男生人数是六年级男生人数的$\frac{9}{2}$倍。因此，五年级男生人数 = $\frac{9}{2}\times12 = 54$所以，五年级有54名男生。
已知：方程组：$8a+20b=1$ 和 $9a+18b=1$求解：用消元法解方程组。解：已知方程组为：$8a+20b=1$ ......... $( i)$$9a+18b=1$ .........$( ii)$将$( i)$乘以9，$( ii)$乘以8，得$72a+180b=9$ ........ $( iii)$$72a+144b=8$ ....... $( iv)$$( iii)$减去$( iv)$，得$72a+180b-72a-144b=9-8$$\Rightarrow 36b=1$$\Rightarrow b=\frac{1}{36}$，将此值代入$( i)$，得$8a+20\times\frac{1}{36}=1$$\Rightarrow 8a+\frac{20}{36}=1$$\Rightarrow 8a+\frac{5}{9}=1$$\Rightarrow 8a=1-\frac{5}{9}$$\Rightarrow 8a=\frac{9-5}{9}$$\Rightarrow 8a=\frac{4}{9}$$\Rightarrow a=\frac{4}{9}\times\frac{1}{8}$$\Rightarrow a=\frac{1}{18}$因此，$a=\frac{1}{18}$，$b=\frac{1}{36}$。
已知：\( \frac{6 y-5}{2 y}=\frac{7}{9} \)求解：求y的值。解：$\frac{6 y-5}{2 y}=\frac{7}{9}$$\Rightarrow 9(6y-5)=7(2y)$ (交叉相乘)$\Rightarrow 54y-45=14y$$\Rightarrow 54y-14y=45$ $\Rightarrow 40y=45$$\Rightarrow y=\frac{45}{40}$$\Rightarrow y=\frac{9}{8}$y的值为$\frac{9}{8}$。