数据结构
网络
关系型数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
已知：一头小牛用一根长 6 米的绳子系在一个边长为 20 米的正方形草坪的一个角上。绳子的长度增加了 5.5 米。要求：我们必须找到小牛可以吃草的草坪面积的增加量。解答：假设小牛系在正方形草坪的 A 角上。面积的增加量等于两个中心角分别为 90 度，半径分别为 (6 + 5.5) 米 = 11.5 米和 6 米的扇形面积之差，即阴影区域... 阅读更多
已知：一头小牛用一根长 6 米的绳子系在一个边长为 20 米的正方形草坪的一个角上。绳子的长度增加了 5.5 米。要求：我们必须找到小牛可以吃草的草坪面积的增加量。解答：方形水箱的边长 = 40 米每个半圆形草坪的半径 = 40/2 米 = 20 米每平方米铺设草坪的费用 = 1.25 元半径为 r 的半圆形面积为 1/2πr^2。因此，方形周围四个半圆形草坪的面积 = 4 × ... 阅读更多
已知：一个长方形公园长 100 米，宽 50 米。公园周围环绕着半圆形的花坛。要求：我们必须找到平整半圆形花坛的费用。解答：长方形公园的长 l = 100 米长方形公园的宽 b = 50 米沿着长边每个半圆形花坛的半径 r1 = 100/2 = 50 米沿着宽边每个半圆形花坛的半径 r2 = 50/2 = 25 米因此，长边上两个半圆的面积 = 2 × 1/2πr1^2 = 3.14 × (50)^2 米^2 = 3.14 × 2500 米^2 = 7850 米^2宽边上两个半圆的面积 = 2 × 1/2πr2^2 = 3.14(25)^2 ... 阅读更多
已知：一头牛用一根长 14 米的绳子系在一个长 20 米，宽 16 米的长方形草地的角落。要求：我们必须找到牛可以吃草的草地面积。解答：牛可以吃草的面积 = 半径为 14 米的圆的 1/4 面积。= 1/4 × πr^2 = 3.14 × 14 × 14 / 4 = 153.86 米^2牛可以吃草的面积为 153.86 米^2。
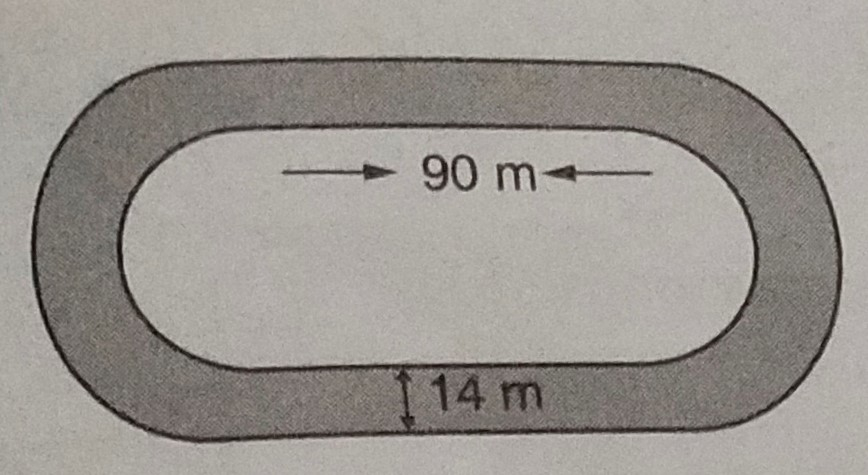
"\已知：一条跑道的内圈周长为 400 米。每段直线的长度为 90 米，两端为半圆形。跑道处处宽 14 米。要求：我们必须找到跑道的面积和外圈跑道的长度。解答：每个半圆形部分的周长 = [400 - (90 + 90)] / 2 = [400 - 180] / 2 = 220 / 2 = 110 米设 r 为内半圆的半径。这意味着，1/2 × 2πr = 110 ⇒ 22/7 r = 110 ⇒ r = 110 × 7 / 22 ⇒ r = 35 米跑道的宽度 = 14 米这意味着，跑道的外半径 r = 35 + 14 = 49 米内外两条直线之间的长度差 = 14 米外圈两个半圆形的长度 = 2 × [1/2 × 2 × π × (35 + 14)] = 2 × π × 49 = 2 × 22/7 × 49 = 308 米... 阅读更多
镜子和透镜的区别如下：镜子透镜1.它是一块闪亮的玻璃，背面镀银，以便通过反射产生清晰的图像。1.它是一块透明的玻璃或塑料，由两个表面构成，通过两个表面的任何一个表面上的折射产生图像。2.它可以是平面或球面（凹面和凸面）。2.它通常是弯曲的，一侧或两侧弯曲。3.它遵循反射定律。3.它遵循折射定律。4.它可以由玻璃或金属制成。4.它可以由... 阅读更多
不，完全不行，因为凹面镜需要一个向内凹陷的表面或弯曲的反射面。凹面镜是曲面镜的一个例子，曲面镜是球面镜的一部分。
(a)白色物体，如白纸、雪、牛奶、白粉笔、白色珍珠和白色衣服，反射阳光中的所有颜色，因此看起来是白色的。(b)黑色物体，如煤、木炭、焦油、墨水、黑板和黑色衣服，吸收阳光中的所有颜色，因此看起来是黑色的。
彩虹的形成是自然界中证明白光是由不同颜色组成的证据。当太阳照耀并且同时下雨时，由于大气中数百万雨滴（或水滴）对白光的色散，天空就会形成彩虹。每个雨滴都像一个微小的玻璃棱镜，将白光分解成光谱（不同的颜色）。白光中存在的不同颜色光线在穿过水滴时会以不同的角度发生折射或弯曲。因此，白光被分离…… 阅读更多
已知：给定的多项式是 $x^3+ax^2+bx-30$。2 和 3 是 $x^3+ax^2+bx-30$ 的零点。要求：我们需要求出 a 和 b 的值。解：2 和 3 是 $x^3+ax^2+bx-30$ 的零点。当 $x = 2$ 时，$g(2) = (2)^3 + a(2)^2 + b(2) - 30 = 0$。$8+4a + 2b - 30 = 0$$4a + 2b = 22$$2(2a+b)=2(11)$$2a+b=11$-----(i)当 $x =3$ 时，$g(3) =(3)^3 + a(3)^2 + b(3) - 30 = 0$$27+9a + 3b - 30 = 0$$9a + 3b = 3$$3(3a+b)=3$$3a+b=1$----(ii)用 (ii) 减去 (i)，得到 $(3a+b)-(2a+b) = 1-11$$3a-2a = -10$$a=-10$将 $a = -10$ 代入方程 (i)$2(-10)+b = 11$$-20+b =11$$b = 11+20$$b = 31$。…… 阅读更多