已知:$ABCD$ 是一个风筝,并且 $\angle A=\angle C$ 且 $\angle CAD=60^{\circ}$ 且 $\angle CBD=45^{\circ}$。求解:求:$( a).\ \angle BCD$ $( b).\ \angle CDA$ 解:考虑两条对角线的交点为 $O$。在 $\vartriangle AOD$ 和 $\vartriangle COD$ 中,$AD=CD$ [风筝的邻边相等]$AO=CO$ [BD 平分 AC]$OD=OD$ [公共边]$\therefore \vartriangle AOD\cong\vartriangle COD$因此,$\angle CAD=\angle ACD=60^o$在 $\vartriangle ACD$ 中使用角和性质,$\angle CAD+\angle ACD+\angle CDA=180^o$$\Rightarrow 60+60+\angle CDA=180$$\Rightarrow \angle CDA=180-120$$\Rightarrow \angle CDA=60^o$在 $\vartriangle AOB$ 和 $\vartriangle COB$ 中,$AO=CO$ [BD 平分 AC]$OB=OB$ ... 阅读更多
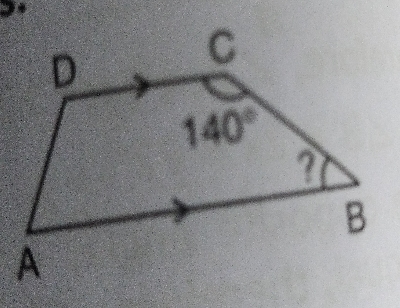
已知:如图所示梯形 $ABCD$。求解:求 $\angle ABC=?$ 解:如图所示,在梯形 $ABCD$ 中,$AB||CD$ 并且 $BC$ 和 $AD$ 不平行。两个邻角之和等于 $180^o$$\Rightarrow \angle ABC+\angle BCD=180^o$$\Rightarrow \angle ABC+140^o=180^o$$\Rightarrow \angle ABC=180^o-140^o=40^o$
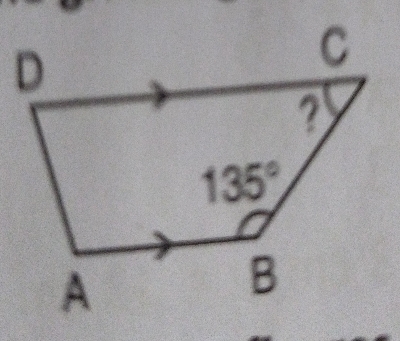
已知:梯形 $ABCD$。求解:求 $\angle C=?$ 解:在梯形 $ABCD$ 中,$\angle B+\angle C=180^o$$\Rightarrow \angle 135^o+\angle C=180^o$$\Rightarrow \angle C=180^o-135^o$$\Rightarrow \angle C=65^o$因此,$\angle C=65^o$。
要找到给定数字中最大的数字,我们应该将给定数字按升序排列。在升序排列中,最后一位数字将是最大的数字。例如:$a$
求解:求 0 的加法逆元。解:0 的加法逆元 = 0 - 0 = 0 因此,0 的加法逆元是 0。
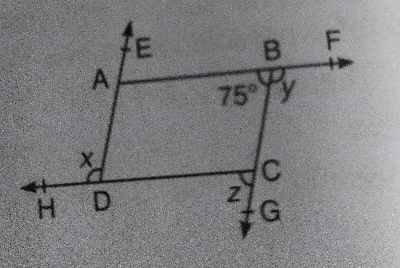
已知:平行四边形 $ABCD$。求解:求 $x$、$y$ 和 $z$。解:$AB||CD$,$\angle ABC=\angle DCG$ [同位角]$\Rightarrow z=75^o$$\angle CBF=\angle XCG$ [内错角]$\Rightarrow y=z=75^o$$\angle ADH=\angle DCG$ [同位角]$x=z=75^o$因此,$x=y=z=75^o$。
渗透作用是指水从水浓度较高区域移动到水浓度较低区域的过程。渗透作用涉及水分子移动,而扩散作用涉及溶质粒子跨浓度梯度的移动。此外,渗透作用需要半透膜来选择性地允许只有水分子而不是溶质粒子移动。影响渗透作用的因素有:压力、温度、浓度梯度、表面积和水势。[额外信息:质壁分离是指植物细胞由于渗透作用而失去细胞质水分并收缩的过程。质壁分离是收缩或 ... 阅读更多
(a) 以下是本案例中为狮子提供食物的食物链:植物 → 鹿 → 人 → 狮子 (b) 如果狮子没有得到猎人作为猎物,它可以寻找食草动物,例如野牛或斑马。(c) 森林中任何顶级消费者,例如老虎或蟒蛇,都可以代替狮子。(d) 在食物链 植物 → 山羊 → 人 中,人是顶级消费者(第一 ... 阅读更多
已知:从地面上的点\( P \)看,一座\( 10 \mathrm{~m} \)高的建筑物的仰角为\( 30^{\circ} \)。在建筑物的顶部竖起一面旗帜,从\( P \)点看旗杆顶部的仰角为\( 45^{\circ} \)。求解:我们必须找到旗杆的长度和建筑物到点\( P \)的距离。解:设 $AB$ 为高大的建筑物,$BC$ 为旗杆的长度。点 $P$ 为观察点。从图中,$\mathrm{AB}=10 \mathrm{~m}, \angle \mathrm{CPA}=45^{\circ}, ... 阅读更多
已知:在一个水平面上有一座垂直的塔,塔顶上有一根旗杆。在距塔底9米处的一点,旗杆顶端和底端的仰角分别为60°和30°。 求解:我们需要求出塔的高度和安装在其上的旗杆的高度。 解:设AB为塔,BC为塔顶上的旗杆。设D为距塔底9米处的一点。由图可知,AD = 9米,… 阅读更多

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP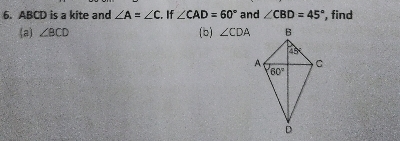 "\
"\
 "\
"\ "\
"\ "\
"\
 "
"