数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
沼气是一种极好的燃料，因为它含有 75% 的甲烷，以及其他气体，如二氧化碳、氢气和硫化氢。解释沼气是由生物质（动物和植物废弃物）在有水但无氧的情况下进行厌氧降解而产生的一种混合气体，其中包括甲烷、二氧化碳、氢气和硫化氢。沼气主要成分是甲烷，甲烷含量高达 75%。
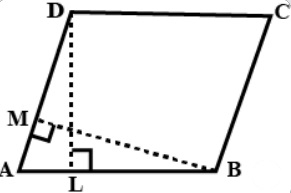
"\已知：平行四边形的面积 $=1470\ cm^2$ $AB=35\ cm$ 和 $AD=49\ cm$求解：我们需要求出 $BM$ 的长度。解：我们知道，底边为 b，高为 h 的平行四边形的面积 $=b\times h$这意味着，$1470=49\times BM$ $BM= \frac{1470}{49}\ cm$$BM=30\ cm$因此，BM 的长度为 30 厘米。
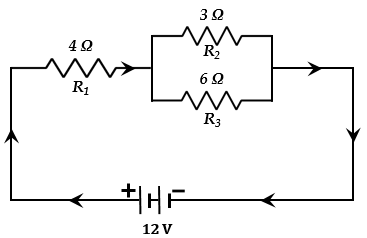
"\已知，电压，V = 12V电阻，R1 = 4Ω，R2 = 3Ω，R3 = 6Ω(i) 要找出电路的总电阻，我们需要将 R1 + R2 + R3 相加。如图所示，电阻 R2 和 R3 并联连接。因此，我们首先将 R2 和 R3 相加，它们的总电阻为：$\frac{1}{R}=\frac{1}{{R}_{2}}+\frac{1}{{R}_{3}}$$\frac{1}{R}=\frac{1}{3}+\frac{1}{6}$$\frac{1}{R}=\frac{2+1}{6}$$\frac{1}{R}=\frac{3}{6}$$\frac{1}{R}=\frac{1}{2}$$R=2\Omega $现在，这个电阻与电阻 R1 串联连接。因此，电路中的总电阻为：${R}_{T}={R}_{1}+({R}_{2}+{R}_{3})$${R}_{T}=4+2$ $\left[\because {R}_{1}=4\Omega \ and\ ({R}_{2}+{R}_{3})=2\Omega \right]$${R}_{T}=6\Omega $ 因此，电路的总电阻为 2 安培。(ii) 流经电路的总电流可以按如下方式计算：$I=\frac{V}{R}$，其中 I = 电流，V ... 阅读更多
已知：$(8x + 4), (6x – 2)$ 和 $(2x + 7)$ 成等差数列。求解：我们需要求出 $x$ 的值。解：如果给定的项成等差数列，则它们的公差相等。因此，$(6x-2)-(8x+4)=(2x+7)-(6x-2)$$6x-8x-2-4=2x-6x+7+2$$-2x-6=-4x+9$$4x-2x=9+6$$2x=15$$x=\frac{15}{2}$ $x$ 的值为 $\frac{15}{2}$。
已知：$x + 1, 3x$ 和 $4x + 2$ 成等差数列。求解：我们需要求出 $x$ 的值。解：如果给定的项成等差数列，则它们的公差相等。因此，$(3x)-(x+1)=(4x+2)-(3x)$$3x-x-1=4x-3x+2$$2x-1=x+2$$2x-x=2+1$$x=3$ $x$ 的值为 $3$。
已知：给定的项为 $(a−b)^2,\ (a^2+b^2),\ (a+b)^2$。求解：我们需要证明 $(a−b)^2,\ (a^2+b^2),\ (a+b)^2$ 成等差数列。解：如果给定的项成等差数列，则它们的公差应该相等。 $( a^2+b^2)−( a−b)^2=(a^2+b^2)−(a^2+b^2−2ab)$$=2ab$$( a+b)^2−( a^2+b^2)=a^2+b^2+2ab−a^2−b^2$$=2ab$因此，$( a^2+b^2)−( a−b)^2=( a+b)^2−( a^2+b^2)$ 因此，给定的项成等差数列。
已知：三个成等差数列的数的和为 $21$，第一个数和第三个数的积比第二个数大 $6$。求解：我们需要求出这三个数。解：设这个等差数列的前三个项为 $a−d, \ a, \ a+d$。根据题目，$a−d+a+a+d=21\ ......( i)$$( a−d)( a+d)=a+6\ .....(ii)$从 $(i)$，我们得到$3a=21$$\Rightarrow a=\frac{21}{3}=7$从 $(ii)$，我们得到$a^2−d^2=a+6\ .....(iii)$将 $a=7$ 代入方程 $(iii)$，我们得到， $(7)^2−d^2=7+6$$\Rightarrow 49−d^2=13$$\Rightarrow 49-13=d^2$$\Rightarrow d^2=36$$\Rightarrow d=6$这意味着， $a-d=7-6=1, a+d=7+6=13, a+2d=7+2(6)=7+12=19$所需的等差数列为 $1, 7, 13, 19......$等差数列的前三个项为 $1, 7$ 和 $13$。阅读更多
已知：三个数成等差数列。这三个数的和为 27，积为 648。求解：我们需要求出这三个数。解：设这个等差数列的前三个项为 $a−d, \ a, \ a+d$。根据题目，$a−d+a+a+d=27\ ......( i)$$( a−d)(a)( a+d)=648\ .....(ii)$从 $(i)$，我们得到$3a=27$$\Rightarrow a=\frac{27}{3}=9$从 $(ii)$，我们得到$a(a^2−d^2)=648\ .....(iii)$将 $a=9$ 代入方程 $(iii)$，我们得到， $9(9^2−d^2)=648$$\Rightarrow 81−d^2=\frac{648}{9}$$\Rightarrow 81-72=d^2$$\Rightarrow d^2=9$$\Rightarrow d=3$这意味着， $a-d=9-3=6, a=9, a+d=9+3=12, a+2d=9+2(3)=9+6=15$所需的等差数列为 $6, 9, 12, 15......$等差数列的前三个项为 $6, 9$ 和 $12$。 阅读更多
已知：四个数成等差数列。这四个数的和为 50，最大的数是最小数的 4 倍。求解：我们需要求出这四个数。解：设这个等差数列的前四个项为 $a-3d, a−d, a+d, a+3d$。根据题目，$a-3d+a−d+a+d+a+3d=50\ ......( i)$$( a+3d)=4(a-3d)\ .....(ii)$从 $(i)$，我们得到$4a=50$$\Rightarrow a=\frac{50}{4}=\frac{25}{2}$从 $(ii)$，我们得到$a+3d=4a-12d$$4a-a=3d+12d$$3a=15d$$a=5d\ .....(iii)$将 $a=5$ 代入方程 $(iii)$，我们得到， $\frac{25}{2}=5d$$\Rightarrow \frac{5}{2}=d$$\Rightarrow d=\frac{5}{2}$这意味着， $a-3d=\frac{25}{2}-3(\frac{5}{2})=\frac{25-15}{2}=\frac{10}{2}=5$$a-d=\frac{25}{2}-\frac{5}{2}=\frac{25-5}{2}=\frac{20}{2}=10$ $a+d=\frac{25}{2}+\frac{5}{2}=\frac{25+5}{2}=\frac{30}{2}=15$ $a+3d=\frac{25}{2}+3(\frac{5}{2})=\frac{25+15}{2}=\frac{40}{2}=20$所需的等差数列为 $5, 10, 15, 20, ......$等差数列的前四个项为 $5, 10, 15$ 和 $20$。 阅读更多
已知：三个数成等差数列。这三个数的和为 12，立方和为 288。求解：我们需要求出这三个数。解：设这个等差数列的前三个项为 $a−d, \ a, \ a+d$。根据题目，$a−d+a+a+d=12\ ......( i)$$( a−d)^3+(a)^3+( a+d)^3=288\ .....(ii)$从 $(i)$，我们得到$3a=12$$\Rightarrow a=\frac{12}{3}=4$从 $(ii)$，我们得到$a^3-d^3-3ad(a-d)+a^3+a^3+d^3+3ad(a+d)=288$$3a^3-3a^2d+3ad^2+3a^2d+3ad^2=288$$3a^3+6ad^2=288$.....(iii)将 $a=4$ 代入方程 $(iii)$，我们得到， $3(4^3+2(4)d^2)=3\times96$$\Rightarrow 64+8d^2=96$$\Rightarrow 8d^2=96-64$$\Rightarrow 8d^2=32$$\Rightarrow d^2=4$$\Rightarrow d=\pm 2$这意味着， 如果 $a=4, d=2$ 则$a-d=4-2=2, a=4, a+d=4+2=6, a+2d=4+2(2)=4+4=8$所需的等差数列为 $2, 4, 6, 8, ......$如果 $a=4, d=-2$ 则$a-d=4-(-2)=4+2=6, a=4, a+d=4+(-2)=2, a+2d=4+2(-2)=4-4=0$所需的等差数列为 $6, 4, 2, 0, ......$这三个数是 ... 阅读更多