数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法学研究
已知：给定的方程组为：$2x+3y=9$ $(p+q)x+(2p-q)y=3(p+q+1)$ 求解：我们需要找到 $p$ 和 $q$ 的值，使得以下线性方程组有无穷多个解。解：给定的方程组可以写成：$2x+3y-9=0$ $(p+q)x+(2p-q)y-3(p+q+1)=0$ 两个变量的方程组标准形式为 $a_{1} x+b_{1} y+c_{1}=0$ 和 $a_{2} x+b_{2} y-c_{2}=0$。将给定的方程组与方程的标准形式进行比较，我们有 $a_1=2, b_1=3, c_1=-9$ 和 $a_2=(p+q), b_2=(2p-q), c_2=-3(p+q+1)$ 给定方程组有无穷多个解的条件是$\frac{a_{1}}{a_{2}} \ =\frac{b_{1}}{b_{2}} =\frac{c_{1}}{c_{2}} \ $$\frac{2}{p+q}=\frac{3}{(2p-q)}=\frac{-9}{-3(p+q+1)}$$\frac{2}{p+q}=\frac{3}{(2p-q)}=\frac{3}{(p+q+1)}$$\frac{2}{p+q}=\frac{3}{2p-q}$ and $\frac{2}{p+q}=\frac{3}{p+q+1}$$(2p-q)\times2=3\times(p+q)$ and $(p+q+1)\times2=3\times(p+q)$$4p-2q=3p+3q$ and $2p+2q+2=3p+3q$$4p-3p=2q+3q$ and $3p-2p+3q-2q=2$$p=5q$ ... 阅读更多
已知：给定的方程组为：$(2 a-1) x-3 y-5=0$ $3 x+(b-2) y-3=0$ 求解：我们需要确定 $a$ 和 $b$ 的值，使得给定的方程组有无穷多个解。解：给定的方程组为：$(2 a-1) x-3 y-5=0$ $3 x+(b-2) y-3=0$ 两个变量的方程组标准形式为 $a_{1} x+b_{1} y+c_{1}=0$ 和 $a_{2} x+b_{2} y-c_{2}=0$。将给定的方程组与方程的标准形式进行比较，我们有 $a_1=(2a-1), b_1=-3, c_1=-5$ 和 $a_2=3, b_2=(b-2), c_2=-3$ 给定方程组有无穷多个解的条件是$\frac{a_{1}}{a_{2}} \ =\frac{b_{1}}{b_{2}} =\frac{c_{1}}{c_{2}} \ $$\frac{2a-1}{3}=\frac{-3}{b-2}=\frac{-5}{-3}$$\frac{2a-1}{3}=\frac{-3}{b-2}=\frac{5}{3}$$\frac{2a-1}{3}=\frac{5}{3}$ and ... 阅读更多
已知：给定的方程组为：$2x-(2a+5) y=5$ $(2b+1)x-9y=15$ 求解：我们需要确定 $a$ 和 $b$ 的值，使得给定的方程组有无穷多个解。解：给定的方程组可以写成：$2x-(2a+5)y-5=0$ $(2b+1)x-9y-15=0$ 两个变量的方程组标准形式为 $a_{1} x+b_{1} y+c_{1}=0$ 和 $a_{2} x+b_{2} y-c_{2}=0$。将给定的方程组与方程的标准形式进行比较，我们有 $a_1=2, b_1=-(2a+5), c_1=-5$ 和 $a_2=(2b+1), b_2=-9, c_2=-15$ 给定方程组有无穷多个解的条件是$\frac{a_{1}}{a_{2}} \ =\frac{b_{1}}{b_{2}} =\frac{c_{1}}{c_{2}} \ $$\frac{2}{2b+1}=\frac{-(2a+5)}{-9}=\frac{-5}{-15}$$\frac{2}{2b+1}=\frac{2a+5}{9}=\frac{1}{3}$$\frac{2}{2b+1}=\frac{1}{3}$ and $\frac{2a+5}{9}=\frac{1}{3}$$2\times3=1\times(2b+1)$ and $3\times(2a+5)=1\times9$$6=2b+1$ and $6a+15=9$$2b=6-1$ and $6a=9-15$$2b=5$ ... 阅读更多
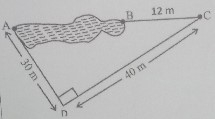
"\已知：如图所示，点 \( A \) 和 \( B \) 位于池塘的两侧。为了找到两点之间的距离，测量员做了一个直角三角形，如图所示。求解：我们需要找到 AB 的距离。解：设 $AB=x$。在图中，$AD=30\ m, DC=40\ m$ 在直角三角形 ADC 中，$AD^2+DC^2=AC^2$$(30)^2+(40)^2=(AB+BC)^2$$900+1600=(x+12)^2$$x^2+144+2(12)x=2500$$x^2+24x+144-2500$$x^2+24x-2356=0$$x^2+62x-38x-2356=0$$x(x+62)-38(x+62)=0$$(x-38)(x+62)=0$$x-38=0$ 或 $x+62=0$$x=38$ 或 $x=-62$$x=38$ （距离不能为负数）因此，A 和 B 两点之间的距离为 38 米。阅读更多
已知：从塔基 4 米和 9 米处，同一直线上两点观察塔顶的仰角互余。求解：我们需要证明塔高为 6 米。解：设塔高为 $TF$，$CF=4\ m$ 和 $DF=9\ m$。设 $\angle TCF=\theta , \angle TDF=90^{o} -\theta$。$\angle TCF+\angle TDF=90^{o}$ (已知)在直角三角形 $\vartriangle TCF$ 中$tan\theta =\frac{TF}{CF}=\frac{TF}{4}$$\Rightarrow TF=4tan\theta \ \ \ \ \ \ \ .................( 1)$在 $\vartriangle TDF$ 中$tan( 90^{o} -\theta ) =\frac{TF}{DF} =\frac{TF}{9}$$\Rightarrow TF=9tan( 90^{o} -\theta )=9cot\theta \ ... 阅读更多
万有引力 (G) 和重力 (g) 之间的区别如下：万有引力 (G)重力 (g)1. 万有引力是作用于宇宙中任意两个物体之间的吸引力。1. 重力是地球对靠近地球表面物体的万有引力。2. 它需要两个质量。2. 它只需要一个质量。3. 它是一种弱力。3. 它是一种强力。4. G 是万有引力常数。4. g 是重力加速度。5. 力， $F=G\frac{M1\times M2}{{R}^{2}}$ (G = 万有引力常数)。5. 力， $F=m\times g$ (g = 重力加速度)。6. G 的值在任何地方都保持不变。(G = 6.673×10-11Nm2/kg2)6. g 的值在地球上的不同位置是不同的。 ... 阅读更多
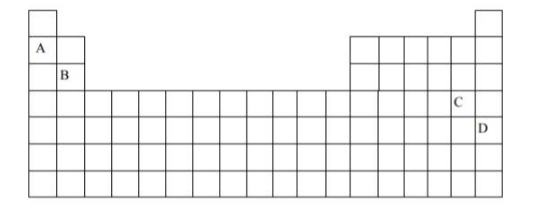
正确答案：(c) C 解释：C 将形成酸性氧化物，因为在元素周期表中，元素 C 占据卤素的位置。A 和 B 是金属，D 是惰性气体。
a) 电池或电池有助于维持导体两端的电势差。b) 电势差定义为将一库仑电荷从一点移动到另一点所做的功。因此，如果将 1 库仑电荷从一点转移到另一点所做的功为 1 焦耳，则称两点间的电势差为 1 伏特。c) 欧姆定律指出，电阻两端的电压与其通过的电流成正比。欧姆定律以德国物理学家格奥尔格·欧姆命名。数学上，这种关系表示为：V = I × R，其中，V = 电压 ... 阅读更多
(a) 建筑物中的电灯应采用并联连接，以便在一个房间中开关灯不会影响同一建筑物中其他灯的运行。这种布置的优点是，如果电路中的设备发生故障或无法工作，则不会影响其他设备。(b) 电熔丝的工作原理利用了电流的热效应。电熔丝设计为只能传输一定量（或安全值）的电流。因此，如果电流超过安全值，导线就会熔断并切断电路 ... 阅读更多