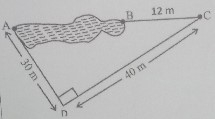
如图所示，点\( A \)和\( B \)位于池塘的相对两侧。为了找到这两点之间的距离，测量员构建了一个如图所示的直角三角形。求距离 AB。
"\n

已知

点\( A \)和\( B \)位于池塘的相对两侧，如图所示。

为了找到这两点之间的距离，测量员构建了一个如图所示的直角三角形。
要求：

我们需要找到距离 AB。

解答

设 $AB=x$。

在图中，

$AD=30\ m, DC=40\ m$
在直角三角形 ADC 中，

$AD^2+DC^2=AC^2$

$(30)^2+(40)^2=(AB+BC)^2$

$900+1600=(x+12)^2$

$x^2+144+2(12)x=2500$

$x^2+24x+144-2500$

$x^2+24x-2356=0$

$x^2+62x-38x-2356=0$

$x(x+62)-38(x+62)=0$

$(x-38)(x+62)=0$

$x-38=0$ 或 $x+62=0$

$x=38$ 或 $x=-62$

$x=38$   (距离不能为负)

因此，点 A 和 B 之间的距离为 38 米。

Tutorialspoint

更新于： 2022 年 10 月 10 日

31 次查看

开启你的 职业生涯

完成课程获得认证

开始学习