在如图所示的菱形 $ABCD$ 中找到 $x$ 的值。
"\n

已知：在给定的图形中，$ABCD$ 是一个菱形，其对角线在点 $O$ 处相交。

求：求 $x$。

解

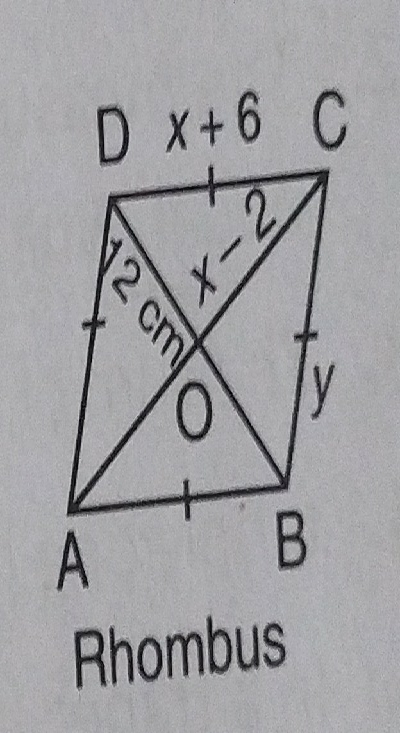
在三角形 $\vartriangle OCD$ 中， 

$OD=12\ cm,\ OC=( x-2)$，且 $CD=( x+6)$

$\angle COD=90^o$    [菱形中，两条对角线在交点处形成 $90^o$ 角$]

应用勾股定理：

$CD^2=OC^2+OD^2$

$\Rightarrow ( x+6)^2=( x-2)^2+12^2$

$\Rightarrow x^2+12x+36=x^2-4x+4+144$

$\Rightarrow 12x+4x=148-36$

$\Rightarrow 16x=112$

$\Rightarrow x=\frac{112}{16}$

$\Rightarrow x=7$

因此，$x=7$。

Tutorialspoint

更新时间： 2022 年 10 月 10 日

40 次浏览

开启你的职业生涯

完成课程获得认证

开始