数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装设计
法律学
已知：在 1 到 100 之间随机选择一个整数。要求：求该整数：$( i)$ 能被 8 整除的概率$( ii)$ 不能被 8 整除的概率解：从 1 到 100 之间随机选择一个整数因此，可能的总结果数 = 100在 1 到 100 之间能被 8 整除的数为 {8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96}有利结果数 = 12$( i)$得到一个能被 8 整除的数的概率 = 有利结果数 / 总结果数 = 12 / 100 = 3 / 25$( ii)。得到一个不能被 8 整除的数的概率 = 有利结果数 / 总结果数 = 1 - 3 / 25 = 22 / 25
"\已知：图 1 中的矩形 ABCD。要求：求 x 和 y 的值。解：因为它是矩形$\therefore AB=CD$$\Rightarrow x+y=30 ...............( 1)$ $AD=BC$$x- y=14 ..............( 2)$将 (1) 和 (2) 相加，得到$x+y+x-y=30+14$$\Rightarrow 2x=44$$\Rightarrow x=\frac{44}{2}$$\Rightarrow x=22$将 x = 22 代入方程 (1)$22+y=30$$\Rightarrow y=30-22$$\Rightarrow y=8$$\therefore x =22\ 和\ y =8$
已知：一年中的假期天数 = 73。要求：我们必须找到假期天数与一年中总天数的比。解：一年中的总天数 = 365。因此，假期天数与一年中总天数的比 = 73:365 = 1:5。
已知：\( \left(8^{0}+5^{-1}\right) \times\left(\frac{1}{5}\right)^{-2} \)要求：我们必须化简给定的表达式。 解：$(8^0+5^{-1})\times(\frac{1}{5})^{-2}=(1+\frac{1}{5})\times(5)^2$ ($a^0=1, (\frac{a}{b})^{-k}=(\frac{b}{a})^k$)$=(\frac{1\times5+1}{5})\times25$$=(\frac{6}{5})\times25$$=6\times5$$=30$因此，$(8^0+5^{-1})\times(\frac{1}{5})^{-2}=(1+\frac{1}{5})\times(5)^2=30$。
已知：$PQ=4.5\ cm, \ \angle P=60^{o}$ 和 $PR=4.5\ cm$. 要求：作图 $\vartriangle PQR$ 并测量 $\angle Q$ 和 $\angle R$。并找到此三角形的类型。解： 按照以下步骤-1. 使用尺子画一条线段 $PQ=4.5\ cm$。2. 使用量角器，画出 $\angle XPQ=60^{o}$。3. 将圆规调整到 $4.5\ cm$ 并标记在 $XP$ 上的点 $R$，其中 $P$ 为圆心。4. 连接 $QR$。$\vartriangle PQR$ 是所需的三角形。使用量角器，当我们测量 $Q$ 和 $R$ 时。我们发现它们都是 $60^{o}$。当我们测量 $QR$ 时，它为 $4.5\ cm$。在这里我们发现... 阅读更多
(i) 磁铁 1 显示 S-N，磁铁 2 显示 N-S。仅供参考的额外信息在磁铁 1 中，磁力线从右侧（北极）开始或发出，因此在左侧，很明显是南极。在磁铁 2 中，磁力线从左侧开始或发出，因此它将是北极，在其对侧（右侧），很明显是南极。 (ii) 磁铁 2 较弱，因为它的磁力线弯曲得更多。换句话说，它的磁... 阅读更多
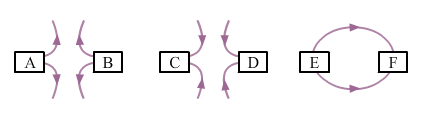
"\第一个示意图：磁力线从A和B开始或发出。这些线也存在排斥。因此，A和B是北极。第二个示意图：磁力线进入或终止于C和D。这些线也存在排斥。因此，C和D是南极。第三个示意图：磁力线从E开始或发出，并进入或终止于F。因此，E是北极，F是南极。
(a) B、C和D每种情况下罗盘针的方向。(b) X是北极。仅供参考的额外信息 在上图中，X是北极，因为磁力线从该侧发出或离开，而Y是南极，因为磁力线进入或进入该侧。