已知:在给定图形中,$DE\ ∥\ BC$ 使得 $AE\ =\ (\frac{1}{4})AC$ 且 $AB\ =\ 6\ cm$。求解:我们需要找到 $AD$。解:在 $\vartriangle ADE$ 和 $\vartriangle ABC$ 中,$\angle A = \angle A$ (公共角)$\angle ADE = \angle ABC$($AB||QR$,同位角)因此,$\vartriangle ADE ∼ \vartriangle ABC$ (根据 AA 相似性)$\frac{AD}{AB} = \frac{AE}{AC}$ (相似三角形对应边成比例)$\frac{AD}{6} = \frac{1}{4}$ ($AE\ =\ (\frac{1}{4})AC$,这意味着,$\frac{AE}{AC} =\frac{1}{4}$) $AD = \frac{6}{4}$ $AD = 1.5\ cm$ $AD$ 的度量值为 $1.5\ cm$。
已知:给定的数字是 690。求解:我们需要将 690 按 2:3:5 的比例分配。解:2:3:5690 需要分成 2 部分、3 部分和 5 部分。总部分数 $=2+3+5=10$。因此,690 应分成 10 部分。所以,一部分 $=\frac{690}{10} = 69$2 部分 $=2 \times 69 = 138$3 部分 $=3 \times 69 = 207$5 部分 $=5 \times 69 = 345$因此,690 应分成 138:207:345。
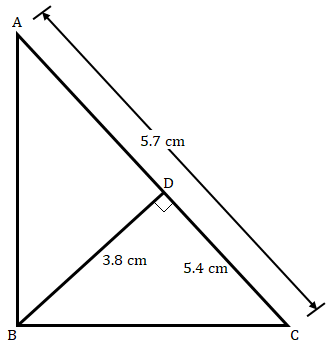
已知:在给定图形中 $∠\ ABC\ =\ 90^o$ 且 $BD\ ⊥\ AC$。$AC\ =\ 5.7\ cm$,$BD\ =\ 3.8\ cm$ 且 $CD\ =\ 5.4\ cm$。求解:我们需要找到 $BC$。解:在 $\vartriangle ABC$ 和 $\vartriangle BDC$ 中,$\angle ABC=\angle BDC=90^o$$\angle C=\angle C$ (公共角)因此,$\vartriangle ABC∼\vartriangle BDC$ (根据 AA 相似性)$\frac{AB}{BD} = \frac{BC}{DC}$ (相似三角形对应边成比例)$\frac{5.7}{3.8} = \frac{BC}{5.4}$$BC = \frac{5.7\times 5.4}{3.8}$$BC = \frac{16.2}{2} = 8.1\ cm$$BC$ 的度量值为 $8.1\ cm$。
已知:在给定图形中 $∠\ ABC\ =\ 90^o$ 且 $BD\ ⊥\ AC$。$BD\ =\ 8\ cm$,且 $AD\ =\ 4\ cm$。求解:我们需要找到 $CD$。解:在 $\vartriangle ABD$ 和 $\vartriangle BCD$ 中,$\angle ABD+\angle DBC=90^o$$\angle C+\angle DBC=90^o$这意味着,$\angle ABD=\angle C$在 $\vartriangle ABD$ 和 $\vartriangle BCD$ 中,$\angle ABD=\angle C$$\angle ADB=\angle BDC=90^o$因此,$\vartriangle DBA∼\vartriangle DCB$ (根据 AA 相似性)$\frac{BD}{CD} = \frac{AD}{BD}$ (相似三角形对应边成比例)$BD^2 = AD \times DC$$(8)^2 = 4 \times DC$$DC = \frac{64}{4} = 16\ cm$$CD$ 的度量值为 $16\ cm$。
已知:$\frac{13}{3}$求解:我们需要找到 $\frac{13}{3}$ 的倒数。解:$\frac{13}{3}$要获得分数的倒数,我们需要交换分子和分母。因此,倒数 $=\ \mathbf{\frac{3}{13}}$所以,$\frac{13}{3}$ 的倒数是 $\frac{3}{13}$。
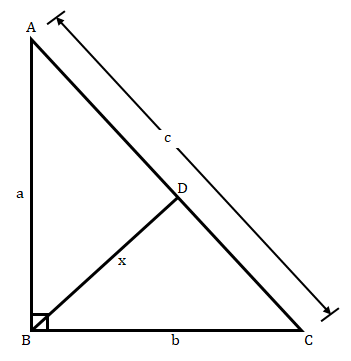
已知:在一个直角三角形中,两条直角边分别为 $a$ 和 $b$,斜边为 $c$,斜边上的高为 $x$。求解:我们需要证明 $ab\ =\ cx$。 解:在给定图形中,$\vartriangle ABC$ 是一个直角三角形,两条直角边分别为 $a$ 和 $b$,斜边为 $c$。设 $BD$ 为斜边 $AC$ 上的高。在 $\vartriangle ACB$ 和 $\vartriangle CDB$ 中,$\angle B = \angle B$ (公共角)$\angle ACB = \angle CDB = 90^o$因此,$\vartriangle ACB ∼ \vartriangle CDB$(根据 AA ... 阅读更多
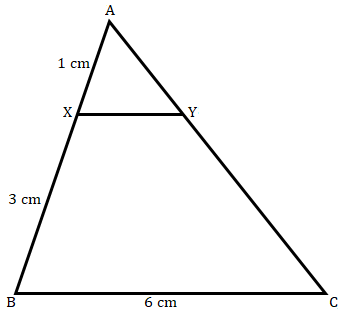
已知:在给定图形中 $XY\ ∥\ BC$。求解:我们需要找到 $XY$ 的长度。解:$AX = 1\ cm, BX = 3\ cm$ 且 $BC = 6\ cm$在 $\vartriangle AXY$ 和 $\vartriangle ABC$ 中,$\angle A = \angle A$ (公共角)$\angle AXY = \angle ABC$($XY||BC$,同位角)因此,$\vartriangle AXY ∼ \vartriangle ABC$ (根据 AA 相似性)因此,$\frac{XY}{BC} = \frac{AX}{AB}$(相似三角形对应边成比例)$\frac{XY}{6} = \frac{1}{1+3}$ ($AB=AX+BX=(1+3)\ cm$)$XY = \frac{6\times1}{4}$$XY = 1.5\ cm$$XY$ 的长度为 $1.5\ cm$。
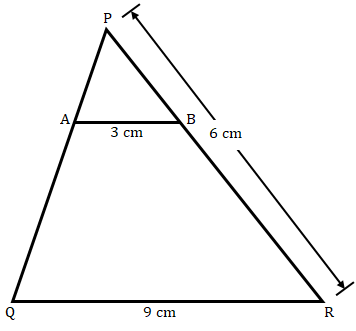
已知:在给定图形中 $AB\ ∥\ QR$。求解:我们需要找到 $PB$ 的长度。解:$AB = 3\ cm, QR = 9\ cm$ 且 $PR = 6\ cm$在 $\vartriangle PAB$ 和 $\vartriangle PQR$ 中,$\angle P = \angle P$ (公共角)$\angle PAB = \angle PQR$($AB||QR$,同位角)因此,$\vartriangle PAB ∼ \vartriangle PQR$ (根据 AA 相似性)因此,$\frac{AB}{QR} = \frac{PB}{PR}$(相似三角形对应边成比例)$\frac{3}{9} = \frac{PB}{6}$$PB = \frac{6}{3}$$PB = 2\ cm$$PB$ 的值为 $2\ cm$。
已知:在给定图形中 $Δ\ ACB\ ∼\ Δ\ APQ$。$BC\ =\ 8\ cm$,$PQ\ =\ 4\ cm$,$BA\ =\ 6.5\ cm$ 且 $AP\ =\ 2.8\ cm$。求解:我们需要找到 $CA$ 和 $AQ$ 的值。解:$Δ\ ACB\ ∼\ Δ\ APQ$ (已知)因此,$\frac{BA}{AQ} = \frac{CA}{AP} = \frac{BC}{PQ}$ (相似三角形对应边成比例)$\frac{6.5}{AQ} = \frac{8}{4}$$AQ = \frac{6.5 \times 4}{8}$$AQ = 3.25\ cm$并且,$\frac{CA}{AP} = \frac{BC}{PQ}$$\frac{CA}{2.8} = \frac{8}{4}$$CA = 2.8 \times 2$$CA = 5.6\ cm$因此,$CA$ 和 $AQ$ 的值分别为 $5.6\ cm$ 和 $3.25\ cm$。
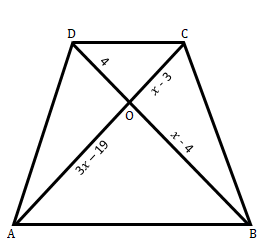
已知:在给定图形中 $AB\ ∥\ CD$。 $OA\ =\ 3x\ –\ 19$,$OB\ =\ x\ –\ 4$,$OC\ =\ x\ -\ 3$ 且 $OD\ =\ 4$。求解:我们需要找到 $x$ 的值。解:我们知道,梯形的对角线将彼此按比例分割。因此,$ \begin{array}{l}\frac{AO}{CO} =\frac{BO}{DO}\\\\\frac{3x-19}{x-3} =\frac{x-4}{4}\\\\4( 3x-19) =( x-4)( x-3)\\\\4( 3x-19) =x( x-3) -4( x-3)\\\\12x -76=x^{2} -3x-4x+12\\\\x^{2} +( -3-4-12) x+( 12+76) =0\\\\x^{2} -19x+88=0\\\\x^{2} -11x-8x+88=0\\\\x( x-11) -8( x-11) =0\\\\( x-11)( x-8) =0\\\\x-11=0\ \ \ or\ \ x-8=0\\\\x=11\ \ \ \ or\ \ \ x=8\end{array}$因此,$x$ 的值为 $8$ 或 $11$。阅读更多

 数据结构
数据结构 网络
网络 关系型数据库管理系统
关系型数据库管理系统 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 语言编程
C 语言编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP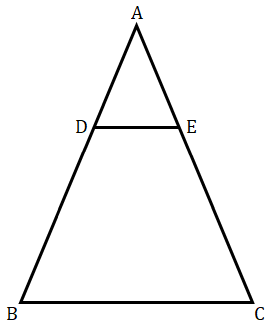 "\
"\
 "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\ "\
"\