在下图中，如果 AB ∥ CD，求 x 的值。

已知

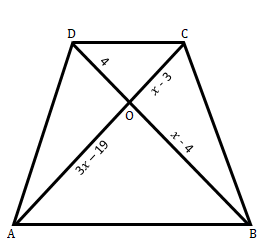
在给定图形中，AB ∥ CD。

OA = 3x – 19，OB = x – 4，OC = x – 3 且 OD = 4。

要求

我们需要求 x 的值。

解答

我们知道：

梯形的对角线将彼此按比例分割。

因此：

$\begin{array}{l} \frac{AO}{CO} =\frac{BO}{DO}\\ \\ \frac{3x-19}{x-3} =\frac{x-4}{4}\\ \\ 4( 3x-19) =( x-4)( x-3)\\ \\ 4( 3x-19) =x( x-3) -4( x-3)\\ \\ 12x -76=x^{2} -3x-4x+12\\ \\ x^{2} +( -3-4-12) x+( 12+76) =0\\ \\ x^{2} -19x+88=0\\ \\ x^{2} -11x-8x+88=0\\ \\ x( x-11) -8( x-11) =0\\ \\ ( x-11)( x-8) =0\\ \\ x-11=0\ \ \ 或\ \ x-8=0\\ \\ x=11\ \ \ \ 或\ \ \ x=8 \end{array}$

因此，x 的值为 8 或 11。

Tutorialspoint

更新于：2022年10月10日

浏览量：33

开启你的职业生涯

完成课程获得认证

开始学习