数据结构
网络
关系数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
已知：一块地板砖的形状是平行四边形，底边为 24 厘米，对应高为 10 厘米。地板面积 = 1080 平方米。求解：我们需要求解覆盖面积为 1080 平方米的地板所需的瓷砖数量。解：一块瓷砖的面积 = 24 厘米 × 10 厘米 = 240 平方厘米。地板面积 = 1080 平方米 = 1080 × (100 厘米)² = 1080 × 10000 平方厘米 = 10800000 平方厘米。所需的瓷砖数量 = 地板面积 / 一块瓷砖的面积 = 10800000 / 240 = 45000。因此，需要 45000 块瓷砖来覆盖地板。
已知：$ 4 \frac{4}{5}+\left\{2 \frac{1}{5}-\frac{1}{2}\left(1 \frac{1}{4}-\frac{1}{4}-\frac{1}{5}\right)\right\} $。求解：解题。$ 4 \frac{4}{5}+\left\{2 \frac{1}{5}-\frac{1}{2}\left(1 \frac{1}{4}-\frac{1}{4}-\frac{1}{5}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{5}{4}-\frac{1}{4}-\frac{1}{5}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{5}{4}-\frac{5-4}{20}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{5}{4}-\frac{1}{20}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{5\times5-1}{20}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{25-1}{20}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{24}{20}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{1}{2}\left( \frac{6}{5}\right)\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{6}{10}\right\} = \frac{24}{5}+\left\{\frac{11}{5}-\frac{3}{5}\right\} = \frac{24}{5}+\left\{\frac{11-3}{5}\right\} = \frac{24}{5}+\left\{\frac{8}{5}\right\} = \frac{24}{5}+\frac{8}{5} = \frac{24+8}{5} = \frac{32}{5} = 6.4 $阅读更多
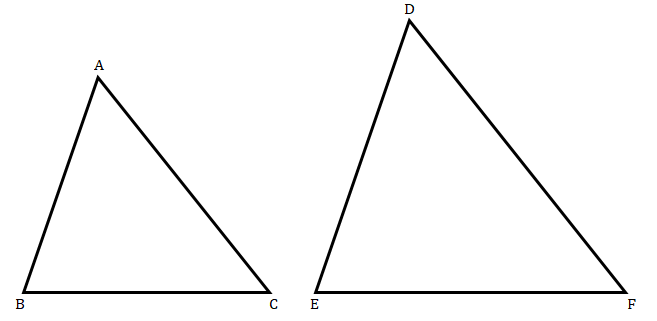
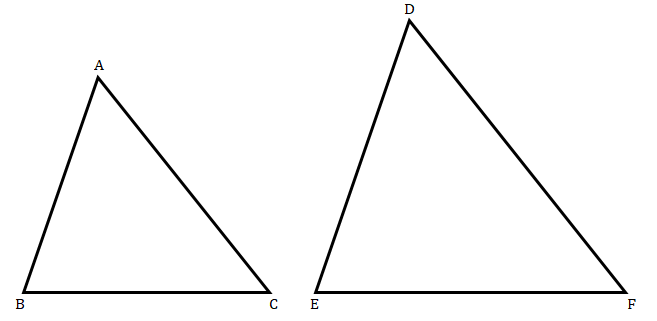
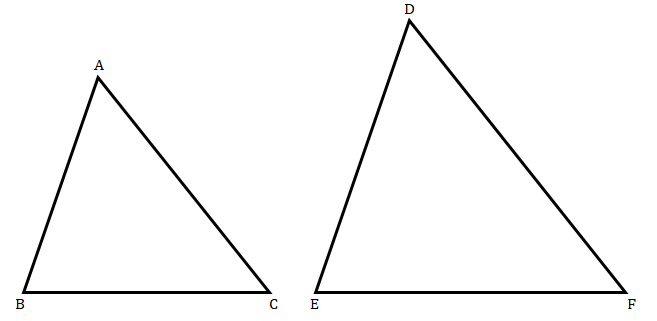
"\已知：三角形 ABC 和 DEF 相似。(ΔABC) 的面积 = 36 平方厘米，(ΔDEF) 的面积 = 64 平方厘米，DE = 6.2 厘米。求解：我们需要求解 AB。解：我们知道，两个相似三角形的面积之比等于它们对应边平方之比。因此，$ \begin{array}{l}\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\left(\frac{AB}{DE}\right)^{2}\\\\\frac{36}{64} =\left(\frac{AB}{6.2}\right)^{2}\\\\\frac{AB}{6.2} =\sqrt{\frac{36}{64}}\\\\AB=\frac{6.2\times 6}{8}\\\\AB=\frac{37.2}{8}\\\\AB=4.65\ cm\end{array}$AB 的值为 4.65 厘米。
"\已知：三角形 ABC 和 DEF 相似。AC = 19 厘米，DF = 8 厘米。求解：我们需要求解两个三角形面积的比值。解：我们知道，两个相似三角形的面积之比等于它们对应边平方之比。因此，$ \begin{array}{l}\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\left(\frac{AB}{DE}\right)^{2}\\\\\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\left(\frac{19}{8}\right)^{2}\\\\\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\frac{361}{64}\end{array}$它们对应边平方的比值为 361/64。
"\已知：三角形 ABC 和 DEF 相似。(ΔABC) 的面积 = 9 平方厘米，(ΔDEF) 的面积 = 64 平方厘米，DE = 5.1 厘米。求解：我们需要求解 AB。解：我们知道，两个相似三角形的面积之比等于它们对应边平方之比。因此，$ \begin{array}{l}\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\left(\frac{AB}{DE}\right)^{2}\\\\\frac{9}{64} =\left(\frac{AB}{5.1}\right)^{2}\\\\\frac{AB}{5.1} =\sqrt{\frac{9}{64}}\\\\AB=\frac{5.1\times 3}{8}\\\\AB=\frac{15.3}{8}\\\\AB=1.9125\ cm\end{array}$AB 的值为 1.9125 厘米。
"\已知：三角形 ABC 和 DEF 相似。(ΔABC) 的面积 = 16 平方厘米，(ΔDEF) 的面积 = 25 平方厘米，BC = 2.3 厘米。求解：我们需要求解 EF。解：我们知道，两个相似三角形的面积之比等于它们对应边平方之比。因此，$ \begin{array}{l}\frac{ar\vartriangle ABC}{ar\vartriangle DEF} =\left(\frac{BC}{EF}\right)^{2}\\\\\frac{16}{25} =\left(\frac{2.3}{EF}\right)^{2}\\\\\frac{EF}{2.3} =\sqrt{\frac{25}{16}}\\\\EF=\frac{5\times 2.3}{4}\\\\EF=\frac{11.5}{4}\\\\EF=2.875\ cm\end{array}$EF 的值为 2.875 厘米。
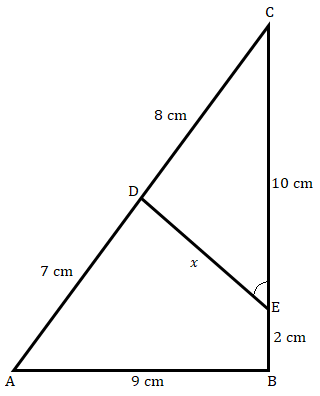
"\已知：在给定图形中，∠A = ∠CED。求解：我们需要证明 ΔCAB ∼ ΔCED 并求 x 的值。解：在 ΔCAB 和 ΔCED 中，∠C = ∠C (公共角) ∠A = ∠CED (已知) 因此，ΔCAB ∼ ΔCED (根据 AA 相似性) 这意味着，$\frac{CA}{CE} = \frac{AB}{DE}$ (对应边成比例) $\frac{15}{10} = \frac{9}{x}$ $x = \frac{9\times 10}{15}$ $x=6\ cm$x 的值为 6 厘米。
已知：电子电荷为 $1.6\times10^{-19}$ C 求：构成2A电流每秒流动的电子数目 解：电流定义为带电粒子流动的速率。因此， $\mathrm{i}=\frac{\mathrm{Q}}{\mathrm{t}}$ 因此，流过的电荷为： $\mathrm{Q}=\mathrm{i} \mathrm{t}$ 所以 $\mathrm{Q}=2 \times 1=2 \mathrm{C}$ 如果 N 是通过的电子数，e 是电子电荷，值为 $1.6 \times 10^{-19}$ 电荷 Q 由电子产生，因此， $\mathrm{Q}=\mathrm{N} \times \mathrm{e}$ 这里 $\mathrm{Q}=2 \mathrm{C}$ 那么， $\mathrm{N}=\frac{\mathrm{Q}}{\mathrm{e}}=\frac{2}{1.6 \times 10^{-19}}$ ... 阅读更多