数据结构
网络
RDBMS
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
用牛粪生产沼气是一种化学变化，因为它是一种不可逆变化，并且无法通过普通的物理方法获得原始反应物。
已知：一个两位数，可以被 5 整除，十位数是 6，并且不是 10 的倍数。 求解：我们需要找到这个两位数。 解答：可以被 5 整除且十位数是 6 的两位数是 60 和 65。 但题目中给定该数不是 10 的倍数。 因此，所需的两位数是 65。
已知：罗纳克有两个盒子，其中-盒子 A 显示放置在其中的数字中奇数数字的数量。 -盒子 B 显示放置在其中的数字中偶数数字的数量。 求解：这里我们需要找到当放在任何一个盒子里都会得到相同答案的数字。 解答：-盒子 A 显示放置在其中的数字中奇数数字的数量。 -盒子 B 显示放置在其中的数字中偶数数字的数量。 如果一个数字在两个盒子里都显示相同的答案，那么 ... 阅读更多
"\已知：$-\frac{2}{3}\ \times\ \frac{3}{5}\ +\ \frac{5}{2}\ -\ \frac{3}{5}\ \times\ \frac{1}{6}$ 求解：这里我们需要求出给定表达式的值。 解答：$-\frac{2}{3}\ \times\ \frac{3}{5}\ +\ \frac{5}{2}\ -\ \frac{3}{5}\ \times\ \frac{1}{6}$ 首先让我们简化每一项：$\frac{2}{3}\ \times\ \frac{3}{5}\ =\ \frac{2}{5}$$\frac{3}{5}\ \times\ \frac{1}{6}\ =\ \frac{1}{10}$ 因此表达式将变为 $=\ -\frac{2}{5}\ +\ \frac{5}{2}\ -\ \frac{1}{10}$ 5、2、10 的最小公倍数：10 根据最小公倍数调整分数：$=\ -\frac{4}{10}\ +\ \frac{25}{10}\ -\ \frac{1}{10}$ 由于分母相等，因此合并分数：$=\ \frac{-\ 4\ +\ 25\ -\ 1}{10}$ 加/减数字：$=\ \frac{20}{10}$ 除以数字： $=\ \mathbf{2}$ 因此，给定表达式的值为 2。
已知：5000 需要做：这里我们需要将 5000 表示为罗马数字。 答案：罗马数字：5000 = $\overline{V}$ 它是在 V 上加了一条横线。 因此，$\overline{V}$ 用于表示罗马数字中的 5000。
已知：长度 = 850 厘米 宽度 = 650 厘米 高度 = 325 厘米 求解：求能完全测量容器尺寸的最长的卷尺 解答：我们需要找到最大公约数 850 的因数 - 2 $\times$ 5 $\times$ 5 $\times$ 17 650 的因数 - 2 $\times$ 5 $\times$ 5 $\times$ 13 325 的因数 - 5 $\times$ 5 $\times$ 13 从上面得到的公因数是 5 $\times$ 5 = 25 所以 25 是 850、650、325 的最大公约数 能精确测量这三个尺寸的最长卷尺是 25 厘米。
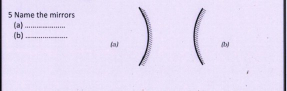
设 $v$ 是图像到镜子或透镜的距离。$u$ 是物体到镜子或透镜的距离。$f$ 是镜子或透镜的焦距。 镜子公式：$\frac{1}{v} + \frac{1}{u} = \frac{1}{f}$ 透镜公式：$\frac{1}{v} - \frac{1}{u} = \frac{1}{f}$
已知：$(-9)\ +\ (+4)\ +\ (-6)\ +\ (+3)$ 需要做：这里我们需要解决给定的表达式。 解答：我们知道，$(+)\ \times\ (-)\ =\ (-)$ 以及 $(-)\ \times\ (-)\ =\ (+)$ $(−9)\ +\ (+4)\ +\ (−6)\ +\ (+3)$ $=\ -9\ +\ 4\ -\ 6\ +\ 3$ $=\ \mathbf{-8}$ 因此，给定表达式的值为 -8。
已知：勾股数 需要解释：这里我们需要解释如何只用一个数字找到勾股数。 解答：如果数字是奇数： 对数字 (n) 进行平方，然后除以 2。 取该数字的前一个和后一个整数，即 $\left(\frac{n^{2}}{2} \ -\ 0.5\right)$ 和 $\left(\frac{n^{2}}{2} \ +\ 0.5\right)$。 勾股数 = n、$\left(\frac{n^{2}}{2} \ -\ 0.5\right)$ 和 $\left(\frac{n^{2}}{2} \ +\ 0.5\right)$。 例子：取数字 n = 3。 对数字进行平方，我们得到 9。 现在取其一半：$\frac{9}{2}$ = 4.5 4.5 之前的整数 = 4 4.5 之后的整数 = 5 ... 阅读更多