
- 大数据分析教程
- 大数据分析 - 首页
- 大数据分析 - 概述
- 大数据分析 - 特征
- 大数据分析 - 数据生命周期
- 大数据分析 - 架构
- 大数据分析 - 方法论
- 大数据分析 - 核心交付成果
- 大数据采用与规划注意事项
- 大数据分析 - 关键利益相关者
- 大数据分析 - 数据分析师
- 大数据分析 - 数据科学家
- 大数据分析有用资源
- 大数据分析 - 快速指南
- 大数据分析 - 资源
- 大数据分析 - 讨论
大数据分析 - 时间序列分析
时间序列是由按日期或时间戳索引的分类或数值变量的一系列观察值组成。股票价格的时间序列就是一个时间序列数据的典型例子。在下表中,我们可以看到时间序列数据的基本结构。在本例中,每小时记录一次观察值。
| 时间戳 | 股票价格 |
|---|---|
| 2015-10-11 09:00:00 | 100 |
| 2015-10-11 10:00:00 | 110 |
| 2015-10-11 11:00:00 | 105 |
| 2015-10-11 12:00:00 | 90 |
| 2015-10-11 13:00:00 | 120 |
通常,时间序列分析的第一步是绘制序列,这通常使用折线图完成。
时间序列分析最常见的应用是使用数据的时序结构预测数值变量的未来值。这意味着,使用可用的观测值来预测未来的值。
数据的时序排序意味着传统的回归方法没有用。为了构建稳健的预测,我们需要考虑数据时序排序的模型。
时间序列分析最广泛使用的模型称为自回归移动平均 (ARMA)。该模型由两部分组成,自回归 (AR) 部分和移动平均 (MA) 部分。该模型通常称为ARMA(p, q) 模型,其中p 是自回归部分的阶数,q 是移动平均部分的阶数。
自回归模型
AR(p) 读作 p 阶自回归模型。数学上写成 -
$$X_t = c + \sum_{i = 1}^{P} \phi_i X_{t - i} + \varepsilon_{t}$$
其中 {φ1, …, φp} 是要估计的参数,c 是一个常数,随机变量 εt 表示白噪声。对参数的值需要一些约束,以便模型保持平稳。
移动平均
MA(q) 表示 q 阶移动平均模型 -
$$X_t = \mu + \varepsilon_t + \sum_{i = 1}^{q} \theta_i \varepsilon_{t - i}$$
其中 θ1, ..., θq 是模型的参数,μ 是 Xt 的期望值,εt, εt − 1, ... 是白噪声误差项。
自回归移动平均
ARMA(p, q) 模型结合了 p 个自回归项和 q 个移动平均项。数学上,该模型用以下公式表示 -
$$X_t = c + \varepsilon_t + \sum_{i = 1}^{P} \phi_iX_{t - 1} + \sum_{i = 1}^{q} \theta_i \varepsilon_{t-i}$$
我们可以看到,ARMA(p, q) 模型是AR(p) 和MA(q) 模型的组合。
为了对模型有一些直观的理解,可以认为方程的 AR 部分试图估计 Xt − i 观测值的参数,以便预测变量 Xt 的值。最终它是过去值的加权平均。MA 部分使用相同的方法,但使用先前观测值的误差 εt − i。所以最终,模型的结果是一个加权平均值。
以下代码片段演示了如何在 R 中实现ARMA(p, q)。
# install.packages("forecast")
library("forecast")
# Read the data
data = scan('fancy.dat')
ts_data <- ts(data, frequency = 12, start = c(1987,1))
ts_data
plot.ts(ts_data)
绘制数据通常是第一步,以了解数据中是否存在时间结构。从图中我们可以看到,每年年底都有强烈的峰值。
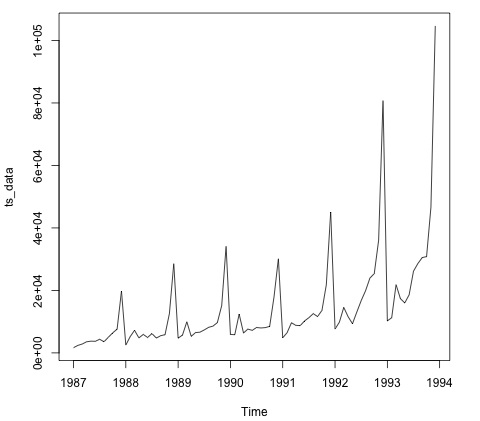
以下代码将 ARMA 模型拟合到数据。它运行了几个模型组合,并选择误差最小的那个。
# Fit the ARMA model fit = auto.arima(ts_data) summary(fit) # Series: ts_data # ARIMA(1,1,1)(0,1,1)[12] # Coefficients: # ar1 ma1 sma1 # 0.2401 -0.9013 0.7499 # s.e. 0.1427 0.0709 0.1790 # # sigma^2 estimated as 15464184: log likelihood = -693.69 # AIC = 1395.38 AICc = 1395.98 BIC = 1404.43 # Training set error measures: # ME RMSE MAE MPE MAPE MASE ACF1 # Training set 328.301 3615.374 2171.002 -2.481166 15.97302 0.4905797 -0.02521172