中心十六边形数

---

十六边形数是指代表十六边形的数字。十六边形是一种由16条边组成的多边形。

中心十六边形数是指由中心的一个点和围绕它以连续的十六边形层（即16边形）排列的其他点所表示的数字。我们可以通过下面的图更好地理解中心十六边形数。

第一个中心十六边形数的中心只有一个点。因此，第一个中心十六边形数为1。

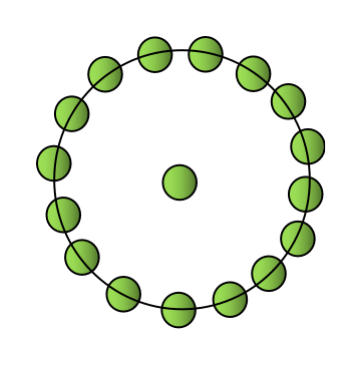
下一个中心十六边形数包含一个中心点和围绕它的一个十六边形。因此，下一个数字将是17。

下一个中心十六边形数将是49，因为中心将有一个点，周围环绕着连续的十六边形层，即16和32。因此，这个数字将是16+32+1=49。

每个第n个中心十六边形数都遵循类似的概念。以此类推，前几个中心十六边形数是**1, 17, 49, 97, 161, 241……**

问题陈述包括我们需要根据给定的输入N打印第N个中心十六边形数。

例如：

输入 : 5

输出 : 161

输入: 8

输出: 449

以下是解决该问题的算法。

算法

对于这个问题，我们需要识别问题中遵循的模式，以便计算第n个中心十六边形数。

中心十六边形数的概念表明，它由中心的一个点和围绕它的连续的十六边形层表示。连续的十六边形层可以表示为16, 32, 48, 64…。如果我们注意形成的模式，它形成了一个公差为16的等差数列。

由于前几个中心十六边形数为1, 17, 49, 97…。如果我们仔细观察这个模式，它只不过是从0和1开始，直到N的连续十六边形层的总和。

从0开始的连续十六边形层的序列将是0, 16, 32, 48, 64…。

• 第一个中心十六边形数是1，即0+1。

• 第二个中心十六边形数是17，即0+16+1。

• 第三个中心十六边形数是49，即0+16+32+1。

• 第四个中心十六边形数是97，它只是直到N（这里是4）和1的连续十六边形层的总和。它可以表示为0+16+32+48+1。

通过以上例子，我们可以认为第n个中心十六边形数是n项等差数列的和，其公差为16，首项为0。为了计算第n个中心十六边形数，它可以写成：

CHn = 等差数列n项和 + 1

$$\mathrm{CH_n\:=\:\frac{n}{2}(2a\:+(n-1)d)+1}$$

𝐶𝐻𝑛= 第n个中心十六边形数

a= 等差数列的首项，为0

d= 等差数列的公差，即16

将所需的值代入上述公式，它可以进一步修改为：

$$\mathrm{CD_n\:=\:\frac{16n}{2}(n-1)+1}$$

$$\mathrm{CD_n\:=\:8n(n-1)+1}$$

我们将使用上面推导的公式来计算我们方法中的第n个中心十六边形数。

方法

• 初始化一个函数来计算第N个中心十六边形数。

• 使用上面推导的公式计算第N个值。

• 我们将初始化一个变量来存储第n个中心十六边形数的值。

• 返回变量，这将是我们需要的输出。

示例

以下是C++中该方法的实现：

#include <iostream>
#include<bits/stdc++.h>

using namespace std;

//function to calculate the nth centred Hexadecagonal number
int CHn(int N){
   int a= 8 * N * (N-1) + 1; //used to store nth centred Hexadecagonal number value
   
   return a; //return the answer
}
int main(){
   int N=5;
   cout<<CHn(N)<<endl;
   
   N=10;
   cout<<CHn(N)<<endl;
   
   N=13;
   cout<<CHn(N)<<endl;
   
   return 0;
}

输出

161
721
1249

**时间复杂度：O(1)**，因为时间是恒定的。

**空间复杂度：O(1)**，因为不需要额外的空间。

结论

在本文中，我们尝试学习中心十六边形数的概念。我们还提出了一种方法，可以为任何正数N打印第N个中心十六边形数。

我希望您觉得本文有助于解决您关于该概念的所有疑问。