中心十三边形数

---

问题陈述指出，我们需要打印任何正数 N 的第 N 个中心十六边形数。

十三边形数是表示自身十三边形的数字。在数学中，十三边形是一种有 13 条边的多边形。

中心十三边形数是可以表示为中心的一个点，然后在其周围依次排列十三边形的其他点，形成连续的十三边形层，十三边形是一个 13 边形。

让我们通过图形更好地理解中心十三边形数的概念。

第一个中心十三边形数可以用中心的一个点表示。因此，第一个中心十三边形数是 1。

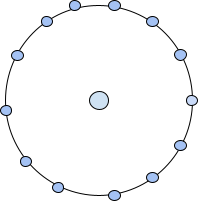
第二个中心十三边形数可以表示为中心的一个点，周围环绕着一个十三边形。因此，第二个中心十三边形数是 14。

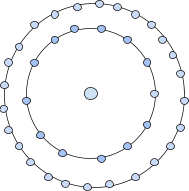
第三个中心十三边形数表示为中心的一个点，周围环绕着一个十三边形，以及一个连续的十三边形层。

因此，这个数字将是 1+13+26=40。

遵循相同的模式，可以找到下一个中心十三边形数。利用中心十三边形数的概念，前几个中心十三边形数为 **1, 14, 40, 79, 131, 196, 274, 365, 469, 586……**。

所以在这个问题中，我们将得到任何正数 N，我们需要打印与 N 值对应的中心十三边形数的值。

示例

输入: 5

输出 : 131

输入: 8

输出 : 365

让我们看看我们将在这个问题中用来解决它的算法。

算法

在这样的问题中，总是有一个遵循的模式。我们需要找出那个模式。每个中心十三边形数都表示为中心的一个点，周围环绕着连续的十三边形层。连续的十三边形层为 13、26、39、52……

如果我们仔细观察十三边形的连续层，我们可以看到它是一个公差为 13 的等差数列。我们可以说第 N 个中心十三边形数是 1 与从 0 开始到 N 的十三边形连续层序列的和的和。

让我们通过下面的插图更好地理解这一点。

从 0 开始的十三边形连续层序列为 0、13、26、39、52……

第一个中心十三边形数是 1，可以表示为 0+1。

第二个中心十三边形数是 14，可以表示为 0+13+1。

第 5 个中心十三边形数是 131，可以表示为从 0 到 5 的十三边形连续层的和，以及 1。

0+13+26+39+52+1= 131.

从上面的例子中，我们可以得出结论，第 N 个中心十三边形数是 1 与等差数列前 N 项和的和，该等差数列的第一项为 0，公差为 13。我们可以将第 N 个中心十三边形数的公式表示为 -

$$\mathrm{(中心十三边形)n\:=\:等差数列前N项和\:+1}$$

$$\mathrm{(中心十三边形)_N\:=\:\frac{N}{2}(2a\:+\:(N-1)d)\:+1}$$

其中，a=等差数列的第一项，为 0

d=等差数列的公差，为 13

$$\mathrm{(中心十三边形)_N\:=\:第N个中心十三边形数}$$

将值代入上述公式后，可以写成

$$\mathrm{(中心十三边形)_N\:=\:(\frac{13N}{2}(N-1))+1}$$

$$\mathrm{(中心十三边形)_N\:=\:\frac{13N(N-1)}{2}+1}$$

每个中心十三边形数都可以表示为 $\mathrm{(\frac{13N(N-1)}{2})+1}$ 的形式。

我们将使用此公式在我们的方法中计算第 N 个中心十三边形数。

方法

我们将用来解决问题的方法的分步说明 -

• 初始化一个函数来计算第 N 个中心十三边形数。

• 使用算法部分推导出的公式查找第 N 个数字并将其存储在任何变量中。

• 返回变量并打印其中存储的值，这将是我们的输出。

示例

C++ 中的方法实现 -

#include <iostream>
#include <bits/stdc++.h>

//function to calculate N-th centred tridecagonal number
long long int CTn(int N){
   long long int ans= ((13 * N * (N-1))/2) + 1; //store the N-th value
   
   return ans; //return the value
}
using namespace std;

int main(){
   int N=12;
   cout<<N<<"-th centred tridecagonal number is : "<<CTn(N)<<endl; //to print the N-th centred tridecagonal number
   N=17;
   cout<<N<<"-th centred tridecagonal number is : "<<CTn(N)<<endl;
   return 0;
}

输出

12-th centred tridecagonal number is : 859
17-th centred tridecagonal number is : 1769

时间复杂度：O(1)，因为执行操作需要常数时间。

空间复杂度：O(1)，没有占用额外的空间。

结论

这就是我们如何使用从观察中心十三边形数序列中遵循的模式推导出的公式来解决上述问题，以便在 C++ 中打印第 N 个中心十三边形数。

我希望您发现本文有助于阐明问题的概念。