中心十五角数

---

问题包括为任何输入数字 N 打印第 N 个中心十五角数。

中心十五角数是一个可以表示为图形形式的数字，该图形在中心有一个点，并被十五边形（即 15 边形）的连续层包围。这里，十五边形的连续层表示围绕中心点的第一层将是 15 边形，下一层将是 30 边形，然后是 45 边形，依此类推。

我们可以通过下面的图形来理解中心十五角数的概念。

第一个中心十五角数用中心的一个点表示。因此，第一个数字将是 1。

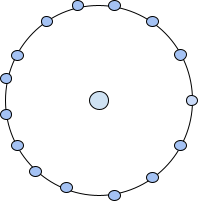
下一个中心十五角数可以表示为中心的一个点，后面跟着一个围绕着的十五边形（15 边形）层。因此，第二个中心十五角数将是 15+1=16。

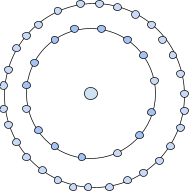
第三个中心十五角数是 46，因为它以图形的形式表示，中心有一个点，周围环绕着十五边形的连续层。十五边形的连续层表明第一层将是 15 边形，第二层将是 30 边形。

我们可以按照相同的模式计算连续的中心十五角数。按照图形中的模式计算出的前几个中心十五角数是1、16、46、91、151、226、316、421、541……。

我们将得到任何正整数 N，我们需要打印对应于该正整数 N 的第 N 个中心十五角数。

示例−

INPUT : N=5
OUTPUT : 151

说明 − 第 5 个中心十五角数是 151，表示为中心的一个点，周围环绕着四层连续的十五边形，其总和为 1+15+30+45+60=151。

INPUT : N=9
OUTPUT : 541

说明 − 第 9 个中心十五角数是 541。

让我们看看算法来找出第 N 个中心十五角数。

算法

我们需要观察中心十五角数序列中遵循的模式。每个第 N 个中心十五角数当表示为图形形式时，都被 (N-1) 个连续的十五边形层包围。十五边形的连续层序列是 15、30、45、60、75……

第一个中心十五角数被 0 个十五边形层包围，因为它只是用中心的一个点表示。所以我们可以说第 N 个中心十五角数是 (N-1) 个连续的十五边形层的总和 + 1。

由于十五边形的连续层序列形成一个公差为 a=15 和公差为 d=15 的等差数列。因此，第 N 个中心十五角数可以计算为 −

$$\mathrm{(centered \: pentadecagonal)_N=sum \: of \: (N − 1)successive \: layers \: of \: pentadecagon + 1}$$

$$\mathrm{sum \: of \: N \: ters \: of \: AP =\frac{N}{2}(2*a+(N − 1)d)}$$

其中，a=等差数列的首项

$$\mathrm{d= 等差数列的公差}$$

使用计算第 N 个中心十五角数的公式，

$$\mathrm{(centered \: pentadecagonal)_N=\frac{(N − 1)}{2}(2*15+(N − 2)*15)+1}$$

$$\mathrm{=\frac{15*(N − 1)}{2}(2+N − 2)+1}$$

$$\mathrm{=\frac{15*N*(N − 1)}{2}+1}$$

这是使用简单数学推导出的获取任何第 N 个中心十五角数的公式。我们将在解决问题的方法中使用此公式。

方法

在 C++ 中应用公式计算第 N 个中心十五角数需要遵循的步骤 −

• 我们将创建一个函数来计算第 N 个中心十五角数。

• 初始化一个名为 ans 的变量为 long long int，以存储较大 N 值的第 N 个中心十五角数。

• 使用算法中推导出的公式计算数字。

• 打印计算出的数字，这将是我们所需的输出。

该方法的 C++ 代码 −

示例

//C++ code to print the N-th centred pentadecagonal number
#include<bits/stdc++.h>
using namespace std;

//function to give the N-th centred pentadecagonal number
long long int Nth_number(int N){
   long long int ans= (15 * N * (N-1))/2 + 1; //to store N-th number
    
   return ans; //return the N-th number
}
int main(){
   int N;
   N=12;
   cout<<"The N-th centred pentadecagonal number is "<<Nth_number(N)<<endl; //calling the function
   N=19;
   cout<<"The N-th centred pentadecagonal number is "<<Nth_number(N)<<endl;
}

输出

The N-th centred pentadecagonal number is 991
The N-th centred pentadecagonal number is 2566

时间复杂度 − O(1)，计算第 N 个数字需要常数时间。

空间复杂度 − O(1)，我们没有使用任何额外的空间。

结论

本文讨论了中心十五角数背后的概念。我们根据中心十五角数序列中遵循的模式，找出了计算任何正数 N 的第 N 个中心十五角数的公式。我们提出了一种有效的方法，使用推导出的公式在 C++ 中打印第 N 个中心十五角数。

我希望在阅读本文后，您对该主题的相关概念已经清楚了。