圆锥

---

引言

圆锥底部有一个曲面；因此，它包含两个表面积，总表面积是圆锥覆盖的总表面积，而曲面面积由曲面覆盖的表面积组成，即除底部圆形平面表面以外的表面积。圆锥有一个顶点或顶端和一条斜高。

在本教程中，我们将讨论圆锥、斜高、曲面面积、总表面积以及一些已解决的示例。

圆锥

圆锥是三维图形，底部有一个圆形平面作为底座，圆周上的线段连接到称为顶点或顶端的点。它的形状像金字塔，但具有圆形横截面而不是三角形横截面。

圆锥是一个三维立体几何物体，顶部有一个尖顶，底部是一个圆形底座。圆锥有一个顶点和一个面。对于圆锥，没有边。

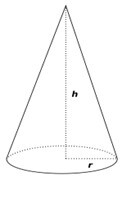
斜高

斜高定义为从顶点或顶端到圆锥圆形底座的距离。斜高的公式是从勾股定理推导出来的，考虑由圆锥的半径、高度和斜高形成的直角三角形。

下图是一个圆锥，其中表示了圆锥的所有尺寸。

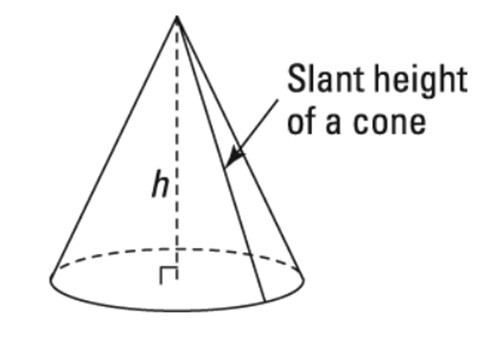
$\mathrm{圆锥的斜高(l)\:等于\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

圆锥的CSA（曲面面积）

曲面面积是在三维平面中由曲面（不包括圆形底座的表面）覆盖的面积。简而言之，称为CSA。

• 曲面面积是不包括平面表面（即圆锥的圆形底座）的面积。

• 曲面面积的公式等于π乘以圆锥的半径乘以圆锥的斜高。它以平方单位测量。

• $\mathrm{圆锥的CSA\:=\:\pi\:\times\:r\times\:l}$

我们知道$\mathrm{圆锥的斜高(l)\:等于\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

$$\mathrm{圆锥的CSA\:=\:\pi\:\times\:r\times\:\sqrt{h^{2}\:+\:r^{2}}}$$

圆锥的TSA（总表面积）

总表面积是在三维平面中由整个圆锥（曲面和平面）覆盖的面积。简而言之，称为TSA。

• 它等于圆锥曲面面积与圆锥圆形底座面积的和。圆形底座的面积等于π乘以圆锥半径的平方。

• 我们现在知道了圆锥的CSA，将π乘以圆锥半径的平方加到CSA中以得到圆锥的TSA。它以平方单位测量。

• $\mathrm{圆锥的TSA\:=\:\pi\:\times\:r\times\:l\:+\:\pi\:\times\:r^{2}}$

$$\mathrm{圆锥的TSA\:=\:\pi\:\times\:r\times\:(l\:+\:r)}$$

我们知道$\mathrm{圆锥的斜高(l)\:等于\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

因此$\mathrm{圆锥的TSA\:=\:\pi\:\times\:r\times\:(\sqrt{h^{2}\:+\:r^{2}}\:+\:r)}$

圆锥的体积

圆锥占据的空间量或容量称为其体积。圆锥的底座是圆形的，因此它由半径和直径组成。然后你可以从底座的中心到圆锥的最顶端部分，这被测量为高度（当然，在冰淇淋的情况下，这个区域在底部）。

• 将圆锥底座的面积乘以圆锥的高度，再乘以三分之一，即可得到圆锥的体积。

• $\mathrm{圆锥的体积\:=\:\frac{1}{3}\pi\:r^{2}h}$

已解决的示例

1) 求半径为2米，高为3米的圆锥的体积？

答案 - 给定半径为2米，高为3米，我们知道立方体的体积为

$$\mathrm{圆锥的体积\:=\:\frac{1}{3}\pi\:r^{2}h}$$

$$\mathrm{圆锥的体积\:=\:\frac{1}{3}\pi\:2^{2}h}$$

$$\mathrm{圆锥的体积\:=4\pi}$$

2) 求半径为2厘米，斜高为4厘米的圆锥的CSA？

答案 - 给定半径为2厘米，斜高为4厘米，我们知道

$$\mathrm{圆锥的CSA\:=\:\pi\:\times\:r\times\:l}$$

$$\mathrm{=\:\pi\:\times\:2\times\:3}$$

$$\mathrm{圆锥的CSA\:=6\pi}$$

3) 如何根据面、边和顶点定义圆锥？

答案 - 2个面，1条边，1个顶点

其中一个面是圆形底座，另一个是连续的曲面。

唯一的一条边是圆形底座的边，两个面在此处相遇。

顶点是顶部的点（尖角）。

4) 求半径为2厘米，斜高为3厘米的圆锥的TSA？

答案 - 给定半径为2厘米，斜高为3厘米

现在应用根据半径和斜高计算圆锥TSA的公式，即

$$\mathrm{圆锥的TSA\:=\:\pi\:\times\:r\times\:l\:+\:\pi\:\times\:r^{2}}$$

$$\mathrm{=\:\pi\:\times\:2\times\:3\:+\:\pi\:\times\:2^{2}}$$

$$\mathrm{=\:10\pi}$$

因此，$\mathrm{圆锥的TSA\:=\:10\pi}$

5) 求高为5厘米，半径为12厘米的圆锥的斜高？

答案 - 给定高为5厘米，半径为12厘米，我们知道

$\mathrm{圆锥的斜高(l)\:等于\:l\:=\:\sqrt{h^{2}\:+\:r^{2}}}$

$$\mathrm{l\:=\:\sqrt{12^{2}\:+\:5^{2}}}$$

$$\mathrm{l\:=\:13}$$

因此$\mathrm{圆锥的斜高(l)\:等于\:l\:=\:13}$

结论

圆锥是一个包含圆形底座的3D图形。它像金字塔；它包含圆形底座，而不是三角形底座。圆锥的表面积是圆锥覆盖的表面。它有两个表面积：曲面面积和总表面积。

常见问题

1. 圆锥是什么意思？

圆锥是三维图形，底部有一个圆形平面作为底座，圆周上的线段连接到称为顶点或顶端的点。

2. 金字塔和圆锥有什么区别？

两者都是具有不同底座的3D图形，金字塔具有三角形底座，而圆锥具有圆形底座

3. 圆锥的斜高是什么意思？

斜高定义为从顶点或顶端到圆锥圆形底座边界的距离。

4. 圆锥有哪些不同类型？

圆锥有两种类型：

• 直圆锥

• 斜圆锥。

5. 斜圆锥是什么意思？

圆锥具有圆形底座，并且顶点和底座的中心不在同一轴线上。顶点不在底座中心的上方。