为表达式-(a + b) * (c + d) - (a + b + c) 构造四元式、三元式和间接三元式
解决方案
首先,此语句将转换为三地址码,如下所示:
t1 = a + b
t2 = -t1
t3 = c + d
t4 = t2 * t3
t5 = t1 + c
t6 = t4 - t5
四元式
| 位置 | 操作符 | 参数 1 | 参数 2 | 结果 |
|---|---|---|---|---|
| (0) | + | a | b | t1 |
| (1) | - | t1 | t1 | |
| (2) | + | t2 | c | d |
| (3) | t3 | t1 | d | * |
| (4) | + | t1 | t2 | t2 |
| (5) | - | * | t2 | t3 |
三元式
| 位置 | 操作符 | 参数 1 | 参数 2 |
| (0) | + | a | b |
| (1) | - | (0) | |
| (2) | + | t2 | c |
| (3) | t3 | (1) | (2) |
| (4) | + | (0) | t2 |
| (5) | - | (3) | (4) |
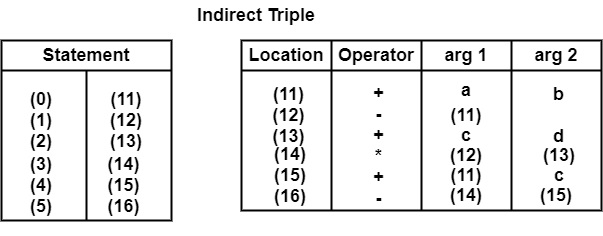
数组表示
四元式是一种最多包含四个字段的结构,即操作符、参数 1、参数 2 和结果。三元式包含三个字段来表示三地址码。三元式的字段包括操作符的名称、第一个源操作数和第二个源操作数。
这种三地址码表示包含三个 (3) 个字段,即一个用于操作符,两个用于参数(即参数 1 和参数 2)。在这种表示中,不使用临时变量。我们不使用临时变量,而是使用括号中的数字来表示指向符号表中该特定记录的指针。
四元式和三元式会导致一些内存浪费,因为某些字段未被占用。为了防止浪费空间,可以使用单个数组来表示表达式。
示例- 考虑语句
a = -b + c * d
其三地址码将为
t1 = -b
t2 = c * d
t3 = t1 + t2
a = t3
四元式将为
| 位置 | 操作符 | 参数 1 | 参数 2 | 结果 |
| (0) | - | b | t1 | |
| (1) | * | t2 | c | t1 |
| (2) | + | t1 | t1 | d |
| (3) | = | d | A |
由于四元式中存在空间浪费,因此可以将其转换为数组表示,如下所示:
| - | B | t1 | t3 | C | c | t1 | + | t1 | t1 | d | = | d | a |
优势
它节省了内存空间。
劣势
它无法识别单词,即它是否是操作符或操作数。在四元式中,可以快速完成此操作,因为操作符和操作数都写在相应的字段中。

广告

 数据结构
数据结构 网络
网络 关系数据库管理系统 (RDBMS)
关系数据库管理系统 (RDBMS) 操作系统
操作系统 Java
Java iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C 编程
C 编程 C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP