余弦 0

---

引言

cos 0 的值为 1。当直角三角形的角度等于零度时，一个称为零度角余弦的数字反映了邻边长度与斜边长度的比率。零度角余弦的精确值等于 1，零度角的余弦用六十进制表示法表示为 cos (0)。

三角函数

数学中的三角函数是将直角三角形的角度与它两条边长的比率联系起来的实函数。它们也称为圆函数。

什么是三角函数

三角函数包括正弦 (sin)、余弦 (cos)、正切 (tan)、余切 (cot)、正割 (sec) 和余割 (csc)，这是用于表示直角三角形边比率的六个数学函数之一。图形显示了这六个三角函数。

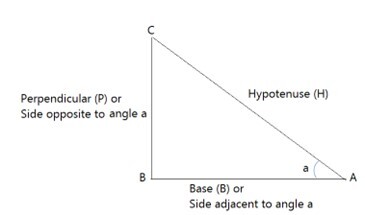
六个基本三角函数

对于一个角，有六个常用的三角函数。它们的名称和缩写分别是正弦 (sin)、余弦 (cos)、正切 (tan)、余切 (cot)、正割 (sec) 和余割 (csc)。

• 正弦函数 - 在三角学中，一个角的正弦函数是指直角三角形的对边（垂直边）与斜边的比率。

  正弦函数公式：对边/斜边 = CB/CA

• 余弦函数 - 余弦（有时缩写为“cos”）是指斜边的长度与邻边长度的比率。

  余弦函数公式：邻边/斜边 = AB/CA

• 正切函数 - 正切函数是六个主要三角函数之一，通常表示为 tan x。在直角三角形中，它考虑的是角的对边和邻边的比率。

  正切函数公式：对边/邻边 = CB/BA

• 正割、余割和余切函数 - 正割、余割 (csc) 和余切是由正弦、余弦和正切导出的三个附加函数。余割 (csc)、正割 (sec) 和余切 (cot) 分别是正弦、余弦和正切的倒数。每个函数都有以下公式：

  • sec a = 1/(cos a) = 斜边/邻边 = CA/AB

  • csc a = 1/(sin a) = 斜边/对边 = CA/CB

  • cot a = 1/(tan a) = 邻边/对边 = BA/CB

余弦函数

在三角形中，邻边与斜边的比率称为余弦函数（或 cos 函数）。余弦是三个基本三角函数之一，是正弦的余角（co-sine）。

余弦函数的特性

余弦的特性取决于角所在的象限。余弦函数是一个独特的三角函数，具有多种特性。以下是其中一些特性：

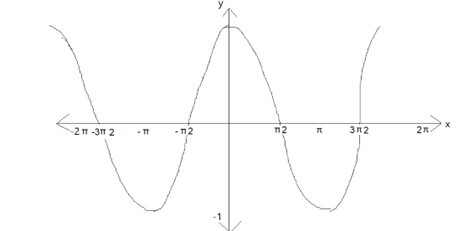
• cos x 图形在周期为 2π 后重复自身，这表明该函数具有周期 2π 并且是周期性的。

• cos(x) = cos(-x)，使其成为偶函数。

• 所有实数都在余弦函数的定义域内，其值域为 [-1,1]。

• 余弦的幂级数展开式为 $\mathrm{cos x =∑_{n=o}^∞(-1)^n \frac{X^{2n}}{(2n)!}}$

余弦函数恒等式

三角学中有多个涉及余弦函数的恒等式。利用这些概念可以有效地解决许多数学问题。以下是其中一些：

• cos x = 1/ sec x

• 当 x 在 [-1, 1] 之间时，余弦函数的反函数为 cos^-1x = arccos x。

• sin²x + cos²x = 1

• cos (x-y) = cos x cos y - sin x sin y

• cos (x+y) = cos x cos y - sin x sin y

• cos 2x = cos² x -sin² x = 2cos² x -1 = 1 - 2sin² x

• 余弦函数积分：∫cosx=sinx+c，其中 C 为积分常数。

余弦 0

众所周知，三角函数是与三角形角度相关的角函数。三角函数已被应用于研究涉及光波和声波的周期性现象。这些函数对于理解谐波振荡和平均温度的波动也至关重要。

圆系统中 cos = 0

在圆系统中，“零”不存在。在圆系统中，每个数字都被视为正数。

cos 0 的百分系统

百分系统共有 100 个单位。第一个单位是 1/100，第二个单位是 1/101。这个模式一直保持到 100。

其他角度的余弦函数

如果已知邻边与斜边的比率，则可以使用反余弦函数计算任何直角三角形的角度。反余弦的符号是 cos^-1⁡x 或 arccos。可以使用 cos 函数计算边长为 1、2 和 3 的直角三角形的角度。

余弦函数的图形

三角比也可以看作是变量的函数，该变量是角度的度量。该角度度量可以用度数或弧度表示。在这里，我们将使用弧度。

例题

1) 求 Sin 45°、Cos 60° 和 Tan 60° 的值。

答案：三角函数表为我们提供：

$$\mathrm{Sin45^\circ =\frac{1}{\sqrt{2}}}$$

$$\mathrm{Cos60^\circ =\frac{1}{2}}$$

$$\mathrm{Tan60^\circ =\sqrt{3}}$$

2) 计算 Sin 105°。

答案：Sin (60° + 45°) 是 sin (105°) 的一种形式，相当于 sin (A + B)。

我们知道 sin 的公式是 sin (A + B) = sin A cos B + cos A sin B

因此，$\mathrm{sin 105^\circ=sin(60^\circ+45^\circ)=sin60^\circ×cos45^\circ+cos60^\circ×sin45^\circ}$

$$\mathrm{=\frac{√3}{2}×\frac{1}{√2}+\frac{1}{2}×\frac{1}{√2}}$$

$$\mathrm{=\frac{√3}{2√2}+\frac{1}{2√2}}$$

$$\mathrm{=\frac{(√3+1)}{2√2}}$$

结论

三角函数是所有三角学的基础。六个三角函数是 sin、cos、tan、csc、sec 和 cot。三角函数用于几何中确定直角三角形的未知边或角。例如，角的对边和斜边都相等。为了快速记住公式，可以使用 SOH CAH TOA。

常见问题

1. Cos 0 符号是什么意思？

0°的余弦是 1。诸如 cos 0°、30°、45°、60° 和 90° 等常用角度的分数值都可以具有正根。

2. 三角函数表有什么用？

您可以查阅三角比表，找到各种三角比（包括 0°、30°、45°、60° 和 90°）的标准角的值。

3. 为什么我们要学习三角学？

使用正弦、余弦、正切等不同的三角函数分析和简化方程是三角学最有效和高级的应用。

4. 三角函数有哪些实际应用？

建筑和施工、通信、电气工程、飞行、GPS、图形、土地测量、音乐和轨迹都使用或包含三角函数。

5. 什么是反余弦？

它是余弦函数的反函数。有时也缩写为“arccos”。当已知直角三角形的两条边的长度时，它用于计算未知角。