如果 $cos\ A = \frac{4}{5}$，那么 $tan\ A$ 的值是
(A) $\frac{3}{5}$
(B) $\frac{3}{4}$
(C) $\frac{4}{3}$
(D) $\frac{5}{3}$

已知

$cos\ A = \frac{4}{5}$

求解

我们需要求 $tan\ A$ 的值。

解：  

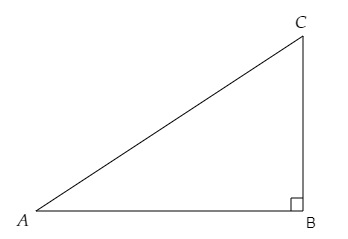
设在直角三角形 $ABC$ 中，$\angle B = 90°$，$cos\ A=\frac{4}{5}$。

我们知道：

在以 $B$ 为直角的直角三角形 $ABC$ 中，

根据勾股定理，

$AC^2=AB^2+BC^2$

根据三角函数定义，

$sin\ \theta=\frac{对边}{斜边}=\frac{BC}{AC}$

$cos\ \theta=\frac{邻边}{斜边}=\frac{AB}{AC}$

$sec\ \theta=\frac{斜边}{邻边}=\frac{AC}{AB}$

$tan\ \theta=\frac{对边}{邻边}=\frac{BC}{AB}$

这里，

$AC^2=AB^2+BC^2$

$\Rightarrow (5)^2=(4)^2+BC^2$

$\Rightarrow BC^2=25-16$

$\Rightarrow BC=\sqrt{9}=3$

因此，

$tan\ A=\frac{BC}{AB}=\frac{3}{4}$。

教程点

更新于：2022年10月10日

64 次浏览

开启你的职业生涯

完成课程获得认证

开始学习