集中趋势的度量：众数、中位数、平均数

---

介绍

集中趋势的度量，也称为中心度量或中心位置度量，是指试图用单个值来表示整个数据集的汇总度量，该值显示分布的中心值。

三种主要的集中趋势度量分别是众数、中位数和平均数。这些值中的每一个都显示了分布中心值的不同的指示。

众数

分布中最常出现的值是众数。考虑一下被选中参加某项比赛的 11 名运动员的年龄。

16,16,16,17,17, 18, 18, 19, 20, 21, 21

下表显示了运动员年龄数据的频数分布

年龄	频数
16	3
17	2
18	2
19	1
20	1
21	2

这里最常见的值是 16。因此，数据的众数是 16 岁。

众数的优点

众数的主要优点是可以计算数值数据和非数值数据。中位数和平均数则不能。

众数的局限性

• 在某些情况下，众数可能无法清楚地表示数据集的中心。当运动员年龄的分布按升序排列时，我们得到

  16,16,16,17,17,18,18, 19,20,21,21

  很容易看出这里的中心值是 18，而不是 16。但是，众数将中心值表示为 16。

• 数据可能有多个众数。考虑以下关于运动员年龄的数据集。

  16,16,16,17,17,18,18,18,19,20,21

  在这里，我们可能得到两个众数——16 和 18。因此，它是**双峰的**。值得注意的是，在大多数情况下也存在**多峰**数据集。因此，在许多情况下，不可能通过众数找到一个集中趋势的度量，因为可能存在多个最常见的数据值。

• 现在，考虑一个连续的数据集。

  16,17,18,19,20,21,22,23,24,25,26

  在这里，运动员年龄的数据是连续的，根本没有众数。因此，对于连续数据集，可能没有众数。

中位数

中位数是数据集在按升序或降序排列时的中间值。

对于运动员的年龄，我们得到按升序排列的数据集

16,16,16,17,17,18,18, 19,20,21,21

这里的中间值是 18。因此，中位数是 18。

当数据集具有偶数个观测值时，两个中间值的平均值作为中位数。考虑以下数据集。

16,16,16,17,17,18,19, 19,20,21,21, 21

此数据集的中位数将是 18 和 19 的平均值，即 18.5。因此，在这种情况下，中位数是 18.5。

中位数的优点

• 中位数通常比平均数受偏斜数据的影响较小。它也较少受异常值的影响。这就是为什么它被认为是用于非对称数据分布集的理想选择。

中位数的局限性

• 中位数的一个缺点是它无法用于分类名义数据，因为很难进行逻辑排序。

平均数

平均数是数据的算术平均值。换句话说，平均数是通过将所有数据加起来，然后将结果除以数据个数获得的。

再次查看运动员的年龄，我们有

16,16,16,17,17, 18, 18, 19, 20, 21, 21

运动员年龄的总和是 16+16+16+17+17+18+18+19+20+21+21=199

现在，将总和除以 11，我们得到 18.09

因此，18.09 是数据集的平均数。

平均数的优点

• 它可用于连续和离散数据集。

平均数的局限性

• 平均数无法用于分类数据，因为数据无法求和。

• 平均数受异常值和偏斜数据的影响，因为它包含所有数据值。

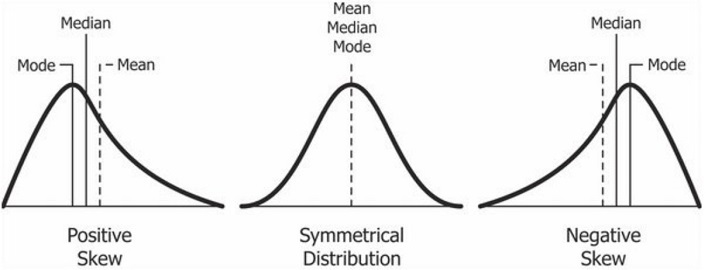
分布的形状如何影响集中趋势

对称分布

当数据集是对称时，众数、中位数和平均数都落在分布的中间。例如，对于更大的运动员年龄数据集，当数据是对称时，平均数、中位数和众数都可能落在 18 岁。

偏斜分布

在偏斜分布的情况下，众数和中位数保持不变，但平均数被拉向尾部。在偏斜分布的情况下，中位数通常是首选的集中趋势，因为平均数不在分布的中心位置。

正偏或右偏分布的右侧尾部比分布的左侧尾部大。在右偏分布的情况下，平均数通常被拉向分布的右侧。在负偏或左偏分布的情况下，平均数被拉向分布的左侧。

异常值如何影响集中趋势的度量

异常值是与数据集中可以找到的一般数据值大相径庭的极端数据值。异常值会改变数据分析的结果，因此在考虑集中趋势的度量时必须检测到它们。

考虑运动员年龄的例子

16,16,16,17,17, 18, 18, 19, 20, 21, 21

假设 90 是一个异常值

考虑包含此异常值的数据

16,16,16,17,17, 18, 18, 19, 20, 21, 90

我们将得到平均值为 16+16+16+17+17+18+18+19+20+21+90=268/11 = 24.36，这与 18.03 大相径庭。因此，结果将是错误的。

有几种回归技术可以识别并从数据集中去除异常值。但是，一般来说，如果确认异常值是极端值并将其从计算中移除，则可以最大限度地减少异常值的影响。

结论

数据集的中心值在经济学和统计学中有很多用途，因为测量中心值可以了解影响各种计算的中心值的频率。因此，学习和应用非常重要。

常见问题

问题 1. 集中趋势的度量是什么意思？

答案。 集中趋势的度量也称为中心度量或中心位置度量，是指试图用单个值来表示整个数据集的汇总度量，该值显示分布的中心值。

问题 2. 集中趋势的度量有哪些三种类型？

答案。 众数、中位数和平均数是集中趋势的三种度量。

问题 3. 哪种集中趋势的度量是数据的算术平均值？

答案。 平均数是数据集的算术平均值。