需要在直径为 13 米的圆形公园边界上竖立一根杆子，使得它到边界上两个直径相对的固定大门 A 和 B 的距离差为 7 米。这是否可行？如果可行，杆子应该离这两个大门多远？

已知

需要在直径为 13 米的圆形公园边界上竖立一根杆子，使得它到边界上两个直径相对的固定大门 A 和 B 的距离差为 7 米。

要求

我们需要找到杆子应该离这两个大门多远。

解答

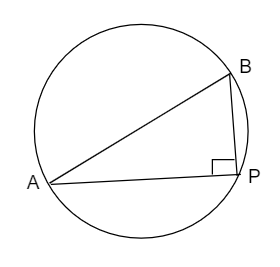
设 P 为杆子的位置，大门 A 到杆子的距离为 x，大门 B 到杆子的距离为 y。

这意味着：

AB = 13 米，且 AP - BP = 7 米

x - y = 7 米

x = y + 7 米

我们知道：

在直角三角形中，斜边的平方等于其他两条边的平方和。（勾股定理）

因此：

AP² + BP² = AB²

(y + 7)² + y² = (13)²

y² + 14y + 49 + y² = 169

2y² + 14y + 49 - 169 = 0

2y² + 14y - 120 = 0

2(y² + 7y - 60) = 0

y² + 7y - 60 = 0

用因式分解法解 y，得到：

y² + 12y - 5y - 60 = 0

y(y + 12) - 5(y + 12) = 0

(y + 12)(y - 5) = 0

y + 12 = 0 或 y - 5 = 0

y = -12 或 y = 5

长度不能为负数。因此，y 的值为 5。

x = 5 + 7 = 12 米

杆子应该离大门 5 米和 12 米。 

教程点

更新于：2022年10月10日

42 次浏览

开启你的职业生涯

完成课程获得认证

开始学习