一根系在18米高垂直杆上的拉线长24米，另一端系着一个桩子。为了使拉线绷紧，桩子应该插在离杆底多远的地方？

已知

一根系在18米高垂直杆上的拉线长24米，另一端系着一个桩子。

要求

我们需要找到为了使拉线绷紧，桩子应该插在离杆底多远的地方。
解答

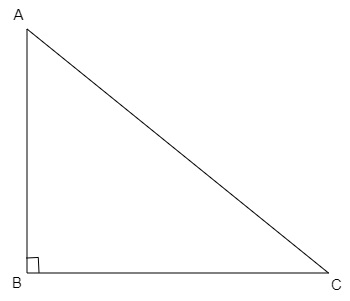
设AB为杆，AC为拉线。

这意味着：

BC是桩子应该插在的位置，以使拉线绷紧。

$AC=24\ 米$ 且 $AB=18\ 米$

$\triangle ABC$是一个直角三角形。因此，根据勾股定理：

$AC^2=AB^2+BC^2$

$(24)^2=(18)^2+BC^2$

$BC^2=576-324$

$BC^2=252\ 米^2$

$BC=\sqrt{252}\ 米$

$BC=\sqrt{36\times7}\ 米$

$BC=6\sqrt7\ 米$

因此，为了使拉线绷紧，桩子应该插在$6\sqrt7\ 米$远的地方。

Tutorialspoint

更新于：2022年10月10日

83 次浏览

启动你的职业生涯

完成课程获得认证

开始