一根高 18 米的旗杆投下 9.6 米长的影子。求旗杆顶端到影子远端的距离。

已知：

一根高 $18\ 米$ 的旗杆投下 $9.6\ 米$ 长的影子。

要求：

求旗杆顶端到影子远端的距离。

解：

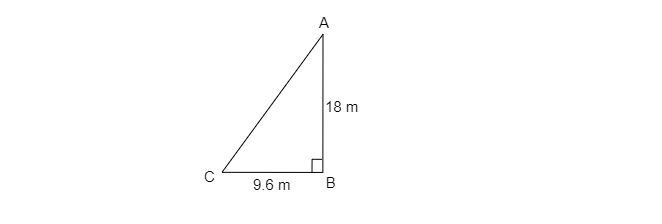
已知旗杆高度 $AB=18\ 米$，影子长度 $BC=9.6\ 米$

旗杆顶端到影子末端的距离为 $AC$。

在 $\vartriangle ABC$ 中，根据勾股定理，

$AC^2=18^2+9.6^2$

$\Rightarrow AC^2=324+92.16$

$\Rightarrow AC^2=416.16$

$\Rightarrow AC^2=( 20.4)^2$

$\Rightarrow AC=20.4\ 米$

因此，旗杆顶端到影子远端的距离为 $20.4\ 米$。

教程点

更新于：2022年10月10日

485 次浏览

开启你的职业生涯

完成课程获得认证

开始学习