""
求 x、y 和 z 的值。
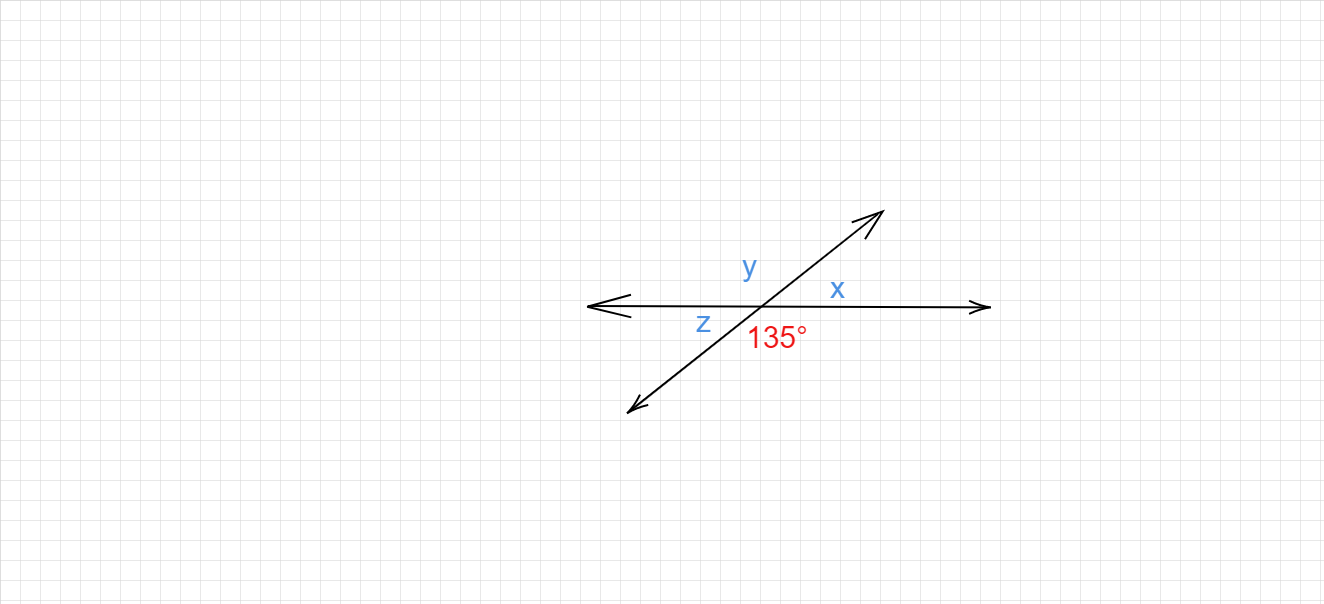
已知
给出了两条相交直线的图形。
要求
我们必须求出 x、y 和 z 的值。
解答
我们知道，
对顶角相等。
一条直线上的角的和为 $180°$。
在给定图形中，
$135°$ 和 y 是对顶角。
因此，
$y = 135°$
$135°$ 和 x 在一条直线上。
这意味着，
$x+135° = 180°$
$x = 180°-135°$
$x = 45°$
$z = x = 45°$ (对顶角)。
- 相关文章
- 求 x、y、z 的值。"
- 在图中，求 $x, y$ 和 $z$ 的值。"
- 求 $x,\ y$ 和 $z$。"
- 在以下每种情况下，求角\( x, y, \) 和 \( z \) 的值:"
- 求 x 和 y 的值。"
- \( \mathrm{RACE} \) 是一个菱形，如图所示。求\( x, y \) 和 \( z \) 的值。"
- 验证给定\( x,\ y \) 和 \( z \) 的值时，属性\( x \times(y+z)=(x \times y)+(x \times z) \) 成立。\( x=\frac{-5}{2}, y=\frac{1}{2} \) 和 \( z=-\frac{10}{7} \)
- 如果\( x=a^{m+n}, y=a^{n+1} \) 和 \( z=a^{l+m} \)，证明\( x^{m} y^{n} z^{l}=x^{n} y^{l} z^{m} \)
- 在\( \Delta X Y Z, X Y=X Z \) 中。一条直线在\( P \) 点与\( X Z \) 相交，在\( Q \) 点与\( Y Z \) 相交，并在\( R \) 点与\( X Y \) 的延长线相交。如果\( Y Q=Y R \) 且\( Q P=Q Z \)，求\( \Delta X Y Z \) 的角。
- 在 C++ 中查找满足 2/n = 1/x + 1/y + 1/z 的 x、y、z。
- 根据附图，求 x 和 y 的值:"
- 在以下矩形中，求 $x$ 和 $y$ 的值。"
- 如果 $x=1,\ y=2$ 和 $z=5$，求 $x^{2}+y^{2}+z^{2}$ 的值。
- 求 $(-3 x y z)(\frac{4}{9} x^{2} z)(-\frac{27}{2} x y^{2} z)$ 的乘积，并验证结果；$x=2, y=3$ 和 $z=-1$
- 从 $5 x y-2 y z-2 z x+10 x y z$ 中减去 $3 x y+5 y z-7 z x$。
数据结构
网络
关系数据库管理系统
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
时尚研究
法律研究
