在△XYZ中，XY=XZ。一条直线分别交XZ于P，交YZ于Q，并与XY的延长线交于R。如果YQ=YR且QP=QZ，求△XYZ的三个角。

已知：

在三角形 XYZ 中，

XY = XZ，YQ = YR；QP = QZ。

求解：

$$\displaystyle \angle XYZ\ ,\ \angle XZY\ ,\ \angle YXZ\ \ $$

解：

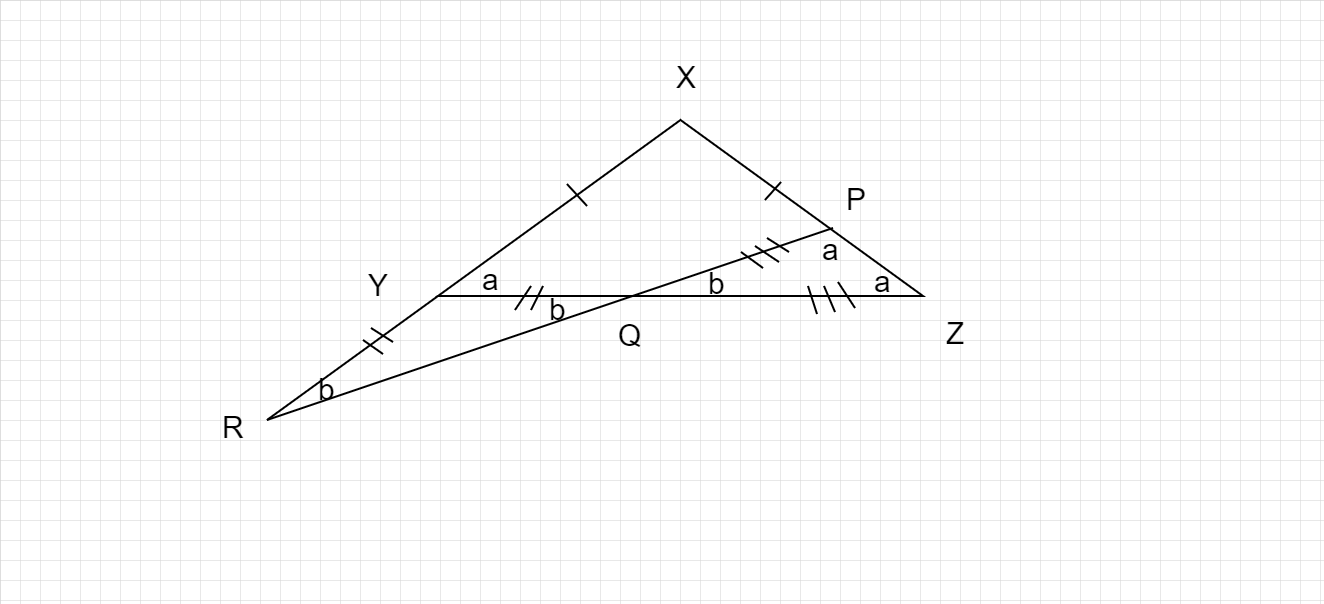
在三角形 XYZ 中，

XY = XZ

因此，设

$\displaystyle \ \angle XYZ\ =\ \angle XZY\ =\ a$

在三角形 YRQ 中，

YQ = YR

因此，设

$\displaystyle \ \angle YQR\ =\ \angle YRQ\ =\ b$

在三角形 PQZ 中，

PQ = QZ

因此，设

$\displaystyle \ \angle PZQ\ =\ \angle QPZ\ =\ a$

对于三角形 YRQ，'a' 是外角，'b'，'b' 是内角。

根据外角性质：

两个内角的和等于与它们不相邻的外角。

$a=b+b$

$a=2b$............................... ( i)

$∠YQR =∠PQZ=b$ (对顶角)

在三角形 PQZ 中，

三角形三个内角的和等于 180°

$a+a+b=180°$

$2a+b=180°$ ...............................( ii)

将 (i) 代入 (ii)

$2a+b=180°$

$2(2b)+b=180°$

$4b+b=180°$

$5b=180°$

$b=\frac{180°}{5}$

$b=36°$

将 b = 36° 代入 (i)

$a=2b$

$a=2\times36°$

$a=72°$

$∠XYZ\ =∠XZY=a$

所以，

∠XYZ = 72° 且

∠XZY = 72°

$\angle XYZ\ \ +\ \angle XZY\ +\ \angle YZX\ =\ 180°$

72° +72° + ∠YZX = 180°

144° + ∠YZX =180°

∠YZX = 180° $-$144°

∠YZX = 36°

因此，三角形 XYZ 的三个角为：

$\angle XYZ =72°$

$\angle XZY =72°$

$\angle YZX =36°$.

教程点

更新时间： 2022年10月10日

301 次浏览

开启您的 职业生涯

通过完成课程获得认证

开始学习