格洛丽亚沿着连接 $(−2,\ 3)$ 和 $(2,\ -2)$ 的路径行走，而苏雷什沿着连接 $(0,\ 5)$ 和 $(4,\ 0)$ 的路径行走。用图形表示这种情况。

已知

格洛丽亚沿着连接  $(−2,\ 3)$  和  $(2,\ -2)$ 的路径行走，而苏雷什沿着连接  $(0,\ 5)$  和  $(4,\ 0)$ 的路径行走。

需要做

我们需要用图形表示上述情况。

解答

对于格洛丽亚的路径

当 $x=-2$ 时，$y=3$

当 $x=2$ 时，$y=-2$

对于苏雷什的路径

当 $x=0$ 时，$y=5$

当 $x=4$ 时，$y=0$

上述情况可以用图形表示如下

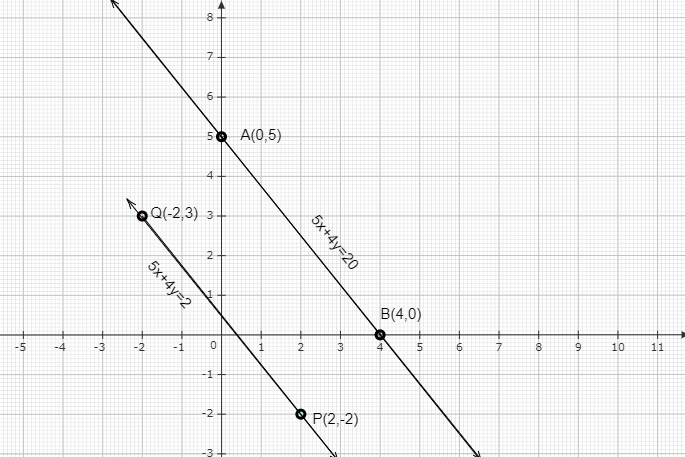
线段 PQ 表示格洛丽亚的路径，线段 AB 表示苏雷什的路径。

教程点

更新于: 2022年10月10日

51 次浏览

开启你的 职业生涯

完成课程获得认证

开始学习