观察旁边的图形，并命名以下内容
(1) 共线点
(2) 射线
(3) 线段
(4) 直线
写出直线的不同名称。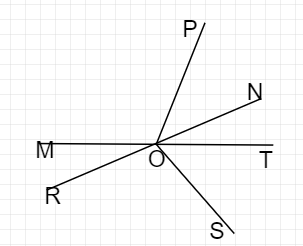
解答
(1) 共线点 R、O、N；M、O、T
(2) 射线：OP、OR、OS；OM、ON、OT
(3) 线段：MO、OT、MT、RO、ON、RN、OP、OS
(4) 直线 RN、MT
2. 直线的不同名称为 l 和 AD
- 相关文章
- 根据下图，写出标注的点和线段的名称。
- 计算下图中的线段数量并命名它们。
- 在下图中，命名以下内容：五条线段。
- 利用图形命名：(a) 五个点 (b) 一条直线 (c) 四条射线 (d) 五条线段
- 命名由三个共线点 P、Q 和 R 确定的线段。
- 找出给定图形中线段的数量。
- 求连接点 $(3, -2)$ 和 $(-3, -4)$ 的线段的三等分点。
- 画一条数轴，并定位以下点：$\frac{1}{2}, \frac{1}{4}, \frac{3}{4}, \frac{4}{4}$
- 求点 $P (\frac{3}{4} , \frac{5}{12})$ 分割连接点 $A (\frac{1}{2}, \frac{3}{2})$ 和 $B (2, -5)$ 的线段的比例。
- 求连接 $(4, -1)$ 和 $(-2, -3)$ 的线段的三等分点的坐标。
- 证明以下点集是共线的。$(1, -1), (2, 1)$ 和 $(4, 5)$
- 求 $a$ 的值，使以下点 $A( a,\ 3),\ B( 2,\ 1)$ 和 $C( 5,\ a)$ 共线。从而求出直线的方程。
- 求连接点 $(2, -2)$ 和 $(-7, 4)$ 的线段的三等分点。
- 在下图中，镜像线（即对称线）用虚线表示。通过在虚线（镜像线）中进行反射来完成每个图形。（你可能需要沿着虚线放置一面镜子，然后在镜子中观察图像）。你能回忆起你所完成的图形的名称吗？
- 确定直线 $2x + y - 4 = 0$ 分割连接点 $A(2, -2)$ 和 $B(3, 7)$ 的线段的比例。
数据结构
网络
关系型数据库管理系统 (RDBMS)
操作系统
Java
MS Excel
iOS
HTML
CSS
Android
Python
C 语言编程
C++
C#
MongoDB
MySQL
Javascript
PHP
物理学
化学
生物学
数学
英语
经济学
心理学
社会学
服装学
法学
